如果你喜欢下棋,你会喜欢学习关于N女王的问题。
什么是 Backtracking?
在追溯中,我们从许多可用的动作中开始一个可能的动作,然后尝试解决问题。
如果我们能够通过选择的移动来解决问题,那么我们会打印解决方案,否则我们会追溯并选择另一个移动,并尝试解决它。
如果没有一个动作奏效,我们声称没有解决问题的办法。
什么是N女王问题?
1How can N queens be placed on an NxN chessboard so that no two of them attack each other?
这种问题常见于 N = 4 和 N = 8。
让我们来看看一个例子,其中 N=4
在解决问题之前,你需要了解象棋女王的运动。
女王可以在任何方向移动任何数量的步骤,唯一的限制是它不能在移动时改变方向。
看看女王的运动,有一点很清楚:没有两位女王可以在同一行或列中。
这允许我们在每个行和每个列中只放置一个女王。
当 N=4时,解决方案看起来如下:
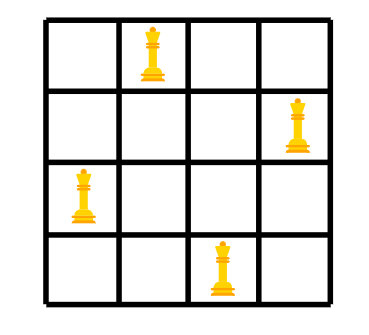
但是,我们怎样才能达成这个安排?
解决N女王问题
我们试图解决这一问题的方法是将女王置于一个位置,并试图排除它被攻击的可能性。
如果我们看到女王在她选择的位置受到攻击,我们尝试下一个位置。
如果一个女王在一连串的所有位置都受到攻击,我们会倒退并更改目前位置之前的女王的位置。
我们重复放置女王和追溯这一过程,直到所有N女王都被成功放置。
逐步退步的步骤如下:
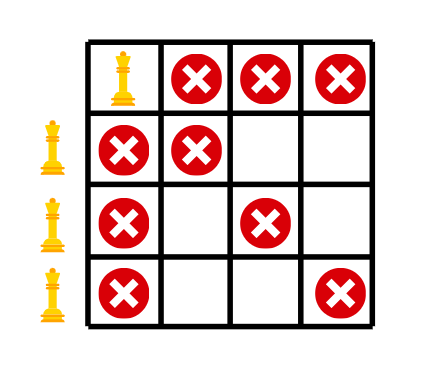
红十字标志着从女王那里攻击的位置. 每当我们到达一个位置,我们有女王要放置,但所有排列中的位置都受到攻击时,我们退步。
这不是唯一可能的解决方案,如果你按时向前迈出每一个女王一步,你就会得到另一个解决方案。
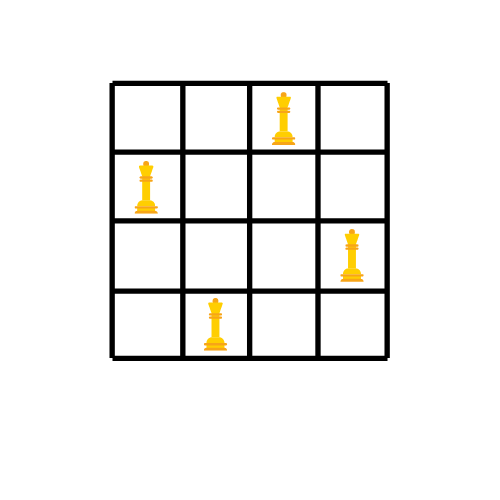
在本示例中,我们按行放置了女王,我们也可以按列方式做同样的事情,在这种情况下,每个女王将属于一个列。
在 C++ 和 Java 中实现 N-Queens 问题
在 C++ 中实现 N-Queens 问题:
1#define N 4
2#include <stdbool.h>
3#include <stdio.h>
4//function to print the solution
5void printSolution(int board[N][N])
6{
7 for (int i = 0; i < N; i++) {
8 for (int j = 0; j < N; j++)
9 printf(" %d ", board[i][j]);
10 printf("\n");
11 }
12}
13
14 // function to check whether the position is safe or not
15bool isSafe(int board[N][N], int row, int col)
16{
17 int i, j;
18 for (i = 0; i < col; i++)
19 if (board[row][i])
20 return false;
21
22 for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
23 if (board[i][j])
24 return false;
25 for (i = row, j = col; j >= 0 && i < N; i++, j--)
26 if (board[i][j])
27 return false;
28
29 return true;
30}
31
32// The function that solves the problem using backtracking
33bool solveNQUtil(int board[N][N], int col)
34{
35 if (col >= N)
36 return true;
37
38 for (int i = 0; i < N; i++) {
39 //if it is safe to place the queen at position i,col -> place it
40 if (isSafe(board, i, col)) {
41
42 board[i][col] = 1;
43
44 if (solveNQUtil(board, col + 1))
45 return true;
46
47 //backtrack if the above condition is false
48 board[i][col] = 0; // BACKTRACK
49 }
50 }
51
52 return false;
53}
54
55// driver program to test above function
56int main()
57{
58 int board[N][N] = { { 0, 0, 0, 0 },
59 { 0, 0, 0, 0 },
60 { 0, 0, 0, 0 },
61 { 0, 0, 0, 0 } };
62
63 if (solveNQUtil(board, 0) == false) {
64 printf("Solution does not exist");
65 return 0;
66 }
67
68 printSolution(board);
69 return true;
70 return 0;
71}
** Java 中的 N-queens 问题实现:**
1package com.JournalDev;
2public class Main {
3 static final int N = 4;
4
5 // print the final solution matrix
6 static void printSolution(int board[][])
7 {
8 for (int i = 0; i < N; i++) {
9 for (int j = 0; j < N; j++)
10 System.out.print(" " + board[i][j]
11 + " ");
12 System.out.println();
13 }
14 }
15
16 // function to check whether the position is safe or not
17 static boolean isSafe(int board[][], int row, int col)
18 {
19 int i, j;
20 for (i = 0; i < col; i++)
21 if (board[row][i] == 1)
22 return false;
23
24 for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
25 if (board[i][j] == 1)
26 return false;
27
28 for (i = row, j = col; j >= 0 && i < N; i++, j--)
29 if (board[i][j] == 1)
30 return false;
31
32 return true;
33 }
34
35 // The function that solves the problem using backtracking
36 public static boolean solveNQueen(int board[][], int col)
37 {
38 if (col >= N)
39 return true;
40
41 for (int i = 0; i < N; i++) {
42 //if it is safe to place the queen at position i,col -> place it
43 if (isSafe(board, i, col)) {
44 board[i][col] = 1;
45
46 if (solveNQueen(board, col + 1))
47 return true;
48
49 //backtrack if the above condition is false
50 board[i][col] = 0;
51 }
52 }
53 return false;
54 }
55
56 public static void main(String args[])
57 {
58 int board[][] = { { 0, 0, 0, 0 },
59 { 0, 0, 0, 0 },
60 { 0, 0, 0, 0 },
61 { 0, 0, 0, 0 } };
62
63 if (!solveNQueen(board, 0)) {
64 System.out.print("Solution does not exist");
65 return;
66 }
67
68 printSolution(board);
69
70 }
71}
1Output :
20 0 1 0
31 0 0 0
40 0 0 1
50 1 0 0

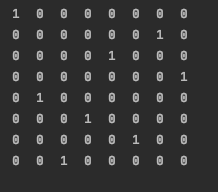
对于 n = 8,输出是:
11 0 0 0 0 0 0 0
2 0 0 0 0 0 0 1 0
3 0 0 0 0 1 0 0 0
4 0 0 0 0 0 0 0 1
5 0 1 0 0 0 0 0 0
6 0 0 0 1 0 0 0 0
7 0 0 0 0 0 1 0 0
8 0 0 1 0 0 0 0 0
理解代码的实施
要检查一个位置是否受到攻击,我们创建了一个名为isSafe的函数。
函数返回真,如果位置是安全的任何攻击。
1static boolean isSafe(int board[][], int row, int col)
2 {
3 int i, j;
4 for (i = 0; i < col; i++)
5 if (board[row][i] == 1)
6 return false;
7
8 for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
9 if (board[i][j] == 1)
10 return false;
11
12 for (i = row, j = col; j >= 0 && i < N; i++, j--)
13 if (board[i][j] == 1)
14 return false;
15
16 return true;
17 }
第一個循環檢查沿著列,第二個和第三個循環檢查沿著兩個直角。
下面的代码负责将女王放在他们的位置并追溯。为了标记女王的位置,我们在矩阵中将该单元格设置为1。
1public static boolean solveNQueen(int board[][], int col)
2 {
3 if (col >= N)
4 return true;
5
6 for (int i = 0; i < N; i++) {
7 //if it is safe to place the queen at position i,col -> place it
8 if (isSafe(board, i, col)) {
9 board[i][col] = 1;
10
11 if (solveNQueen(board, col + 1))
12 return true;
13
14 //backtrack if the above condition is false
15 board[i][col] = 0;
16 }
17 }
18 return false;
19 }
复发式呼叫通过板并设置列为 col+1. 如果复发式呼叫返回错误,我们通过将输入重置为0来反弹。
结论
要了解更多关于追踪的信息,请尝试解决 sudoku 问题。