一个 Min Heap 二进制树是一个二进制树,其根节点在树中具有最小的密钥。
上面的定义适用于树上的所有子树,这被称为 **Min Heap 属性。
除了最后两层之外,几乎每个节点都必须有两个孩子,也就是说,这是一个几乎完整的二进制树,除了最后两层。
下面的树是一个小堆二进制树的例子,因为上面两个属性持有。
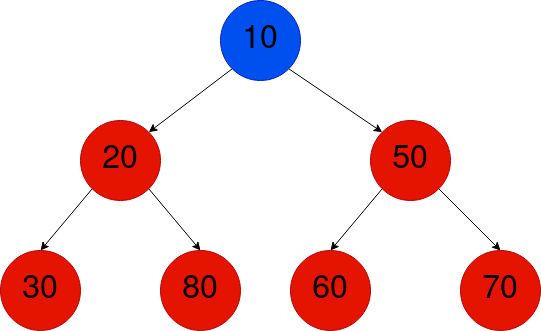
现在我们已经涵盖了什么是矿山堆树,让我们看看我们如何代表它。
代表一个 Min Heap 树
Min Heap 二进制树通常被表示为一个数组,该数组按照下面的格式进行索引:
| Current Node | arr[i] |
| Parent Node | arr[(i-1)/2] |
| Left Child | arr[(2*i) + 1] |
| Right Child | arr[(2*i )+ 2] |
整个树的根在arr[0]。
我们将使用如下图所示的索引,在这里找出与上表相匹配的模式并不难。
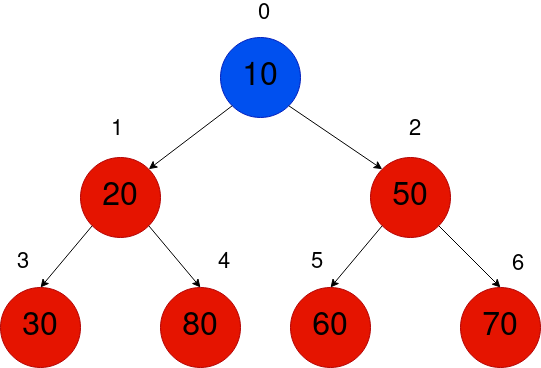
此索引遵循二进制树的 Level Order Traversal,因此一个二进制堆的数组是使用一级订单 Traversal 的二进制树。
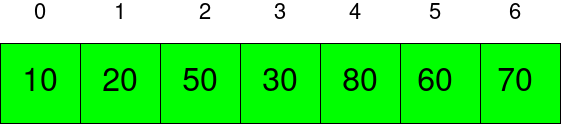
上面的图表显示了Min Heap Tree的数组表示。
现在我们已经涵盖了这些概念,让我们继续在C中实现这一点!
执行一个 Min Heap 树
我们将使用数组表示来构建树木. 让我们开始为 Min Heap 编写结构。
1typedef struct MinHeap MinHeap;
2struct MinHeap {
3 int* arr;
4 // Current Size of the Heap
5 int size;
6 // Maximum capacity of the heap
7 int capacity;
8};
我们将有一组元素和一个大小,随着元素被插入或删除而更新。
数组还具有容量,表示数组的最大大小。
我们需要写一些函数来表示我们代表一棵小树,比如找到父母和孩子。
1int parent(int i) {
2 // Get the index of the parent
3 return (i - 1) / 2;
4}
5
6int left_child(int i) {
7 return (2*i + 1);
8}
9
10int right_child(int i) {
11 return (2*i + 2);
12}
13
14int get_min(MinHeap* heap) {
15 // Return the root node element,
16 // since that's the minimum, by the min-heap
17 // property
18 return heap->arr[0];
19}
我们会写函数来初始化和释放堆栈。
1MinHeap* init_minheap(int capacity) {
2 MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
3 minheap->arr = (int*) calloc (capacity, sizeof(int));
4 minheap->capacity = capacity;
5 minheap->size = 0;
6 return minheap;
7}
8
9void free_minheap(MinHeap* heap) {
10 if (!heap)
11 return;
12 free(heap->arr);
13 free(heap);
14}
有了这一点,现在让我们来谈谈如何插入元素!
插入在我的堆子上
插入算法很简单,将一个元素插入树中。
破解算法:
- 首先,始终在树底插入。插入元素的起始位置是在最后一级 *我们现在需要更新该元素的位置,以便满足min-heap属性
- 由于每个子树的根节点必须是最小的,请检查其直接的母树的子树
- 如果母体大于这个插入元素,我们需要通过交换更新其位置
- 但我们还没有完成,因为更新节点的子树的min-heap属性可能受到侵犯(!
- 我们需要继续交换,直到我们到达根节点,然后我们完成了
为了了解这个过程,让我们举一个例子。
考虑下面的树,只有一个元素。

让我们插入元素40,因为只有一个元素,它插入到底部,我们观察到min-heap属性是满意的,因为10 < 40,所以没有必要交换。
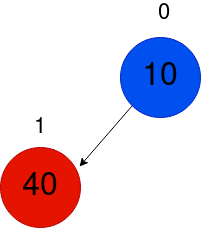
接下来,我们将插入第 50 个,接下来是类似的程序。
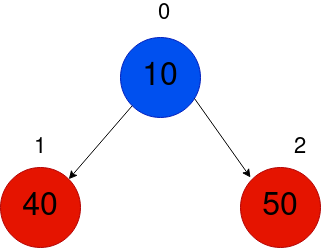
接下来,我们将插入 5,所以现在,我们首先插入到树底,在指数3。
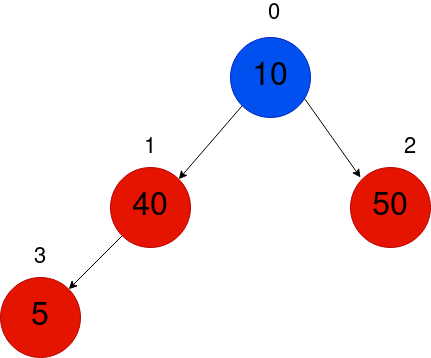
对子树1~3、因此对整棵树来说,小堆的属性被侵犯,所以,我们必须继续与父母交换,直到我们到达根。
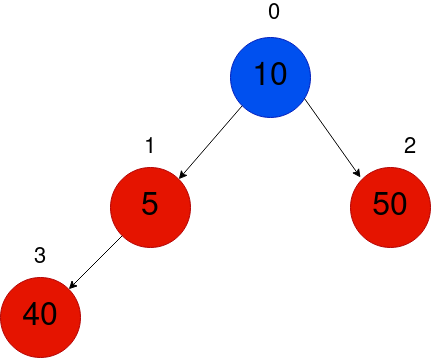
因此,我们需要另一个交换,因为再一次,在0节点根植的子树中,min-heap属性被侵犯。
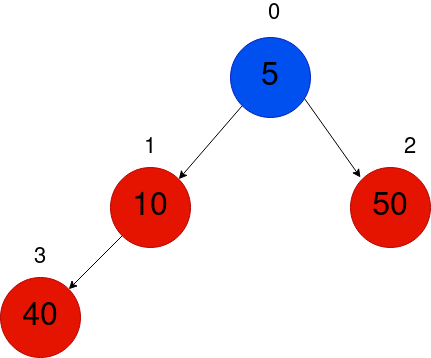
好了!现在我们已经可视化了,让我们把它写下来!
1MinHeap* insert_minheap(MinHeap* heap, int element) {
2 // Inserts an element to the min heap
3 // We first add it to the bottom (last level)
4 // of the tree, and keep swapping with it's parent
5 // if it is lesser than it. We keep doing that until
6 // we reach the root node. So, we will have inserted the
7 // element in it's proper position to preserve the min heap property
8 if (heap->size == heap->capacity) {
9 fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
10 return heap;
11 }
12 // We can add it. Increase the size and add it to the end
13 heap->size++;
14 heap->arr[heap->size - 1] = element;
15
16 // Keep swapping until we reach the root
17 int curr = heap->size - 1;
18 // As long as you aren't in the root node, and while the
19 // parent of the last element is greater than it
20 while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
21 // Swap
22 int temp = heap->arr[parent(curr)];
23 heap->arr[parent(curr)] = heap->arr[curr];
24 heap->arr[curr] = temp;
25 // Update the current index of element
26 curr = parent(curr);
27 }
28 return heap;
29}
现在我们将执行删除方法。
从我的堆中删除
在我们考虑删除一个元素任何索引之前,因为min-heap与根非常密切相关,我们将首先考虑删除根。
要删除最小元素(即根),我们将执行以下操作:
- 更新根作为数组(树)的最后一个元素
- 现在我们将删除底部的最后一个元素. 这类似于在结尾交换和删除! 只是因为我们不再关心根值,我们只是更新它
- 问题再次是我们需要维持min-heap属性
- 所以我们必须确保整个树保持这个属性。
因此,我们知道删除方法将在我们执行heapify()方法后完成。
1MinHeap* delete_minimum(MinHeap* heap) {
2 // Deletes the minimum element, at the root
3 if (!heap || heap->size == 0)
4 return heap;
5
6 int size = heap->size;
7 int last_element = heap->arr[size-1];
8
9 // Update root value with the last element
10 heap->arr[0] = last_element;
11
12 // Now remove the last element, by decreasing the size
13 heap->size--;
14 size--;
15
16 // We need to call heapify(), to maintain the min-heap
17 // property
18 heap = heapify(heap, 0);
19 return heap;
20}
heapify() 程序
该函数采用元素索引索引,并通过交换其直接子树中最小的元素来维持min 堆积属性。
由此产生的树木将满足矿山的财产。
这涉及到找到子树的最小元素,并与当前元素进行交换。
因此,我们需要在最小的元素上反复调用程序,直到我们到达根!
1MinHeap* heapify(MinHeap* heap, int index) {
2 // Rearranges the heap as to maintain
3 // the min-heap property
4 if (heap->size <= 1)
5 return heap;
6
7 int left = left_child(index);
8 int right = right_child(index);
9
10 // Variable to get the smallest element of the subtree
11 // of an element an index
12 int smallest = index;
13
14 // If the left child is smaller than this element, it is
15 // the smallest
16 if (left < heap->size && heap->arr[left] < heap->arr[index])
17 smallest = left;
18
19 // Similarly for the right, but we are updating the smallest element
20 // so that it will definitely give the least element of the subtree
21 if (right < heap->size && heap->arr[right] < heap->arr[smallest])
22 smallest = right;
23
24 // Now if the current element is not the smallest,
25 // swap with the current element. The min heap property
26 // is now satisfied for this subtree. We now need to
27 // recursively keep doing this until we reach the root node,
28 // the point at which there will be no change!
29 if (smallest != index)
30 {
31 int temp = heap->arr[index];
32 heap->arr[index] = heap->arr[smallest];
33 heap->arr[smallest] = temp;
34 heap = heapify(heap, smallest);
35 }
36
37 return heap;
38}
我们现在可以扩展这个delete_minimum()函数,以删除任何元素。
删除任意元素
这只涉及将所需元素设置为最小可能的值,即get_min() - 1,因为它必须小于当前最小值。
我们现在将继续交换,直到我们更新位置,以便新的根是这个元素。
现在,我们又回到了我们旧的 delete_minimum() 函数!我们可以简单地删除新根!
有了这一点,我们的整个删除程序将看起来像这样:
1MinHeap* delete_element(MinHeap* heap, int index) {
2 // Deletes an element, indexed by index
3 // Ensure that it's lesser than the current root
4 heap->arr[index] = get_min(heap) - 1;
5
6 // Now keep swapping, until we update the tree
7 int curr = index;
8 while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
9 int temp = heap->arr[parent(curr)];
10 heap->arr[parent(curr)] = heap->arr[curr];
11 heap->arr[curr] = temp;
12 curr = parent(curr);
13 }
14
15 // Now simply delete the minimum element
16 heap = delete_minimum(heap);
17 return heap;
18}
我现在将向你展示到目前为止的整个代码,以及print()函数,以可视化树。
完整代码
1#include <stdio.h>
2#include <stdlib.h>
3
4typedef struct MinHeap MinHeap;
5struct MinHeap {
6 int* arr;
7 // Current Size of the Heap
8 int size;
9 // Maximum capacity of the heap
10 int capacity;
11};
12
13int parent(int i) {
14 // Get the index of the parent
15 return (i - 1) / 2;
16}
17
18int left_child(int i) {
19 return (2*i + 1);
20}
21
22int right_child(int i) {
23 return (2*i + 2);
24}
25
26int get_min(MinHeap* heap) {
27 // Return the root node element,
28 // since that's the minimum
29 return heap->arr[0];
30}
31
32MinHeap* init_minheap(int capacity) {
33 MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
34 minheap->arr = (int*) calloc (capacity, sizeof(int));
35 minheap->capacity = capacity;
36 minheap->size = 0;
37 return minheap;
38}
39
40MinHeap* insert_minheap(MinHeap* heap, int element) {
41 // Inserts an element to the min heap
42 // We first add it to the bottom (last level)
43 // of the tree, and keep swapping with it's parent
44 // if it is lesser than it. We keep doing that until
45 // we reach the root node. So, we will have inserted the
46 // element in it's proper position to preserve the min heap property
47 if (heap->size == heap->capacity) {
48 fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
49 return heap;
50 }
51 // We can add it. Increase the size and add it to the end
52 heap->size++;
53 heap->arr[heap->size - 1] = element;
54
55 // Keep swapping until we reach the root
56 int curr = heap->size - 1;
57 // As long as you aren't in the root node, and while the
58 // parent of the last element is greater than it
59 while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
60 // Swap
61 int temp = heap->arr[parent(curr)];
62 heap->arr[parent(curr)] = heap->arr[curr];
63 heap->arr[curr] = temp;
64 // Update the current index of element
65 curr = parent(curr);
66 }
67 return heap;
68}
69
70MinHeap* heapify(MinHeap* heap, int index) {
71 // Rearranges the heap as to maintain
72 // the min-heap property
73 if (heap->size <= 1)
74 return heap;
75
76 int left = left_child(index);
77 int right = right_child(index);
78
79 // Variable to get the smallest element of the subtree
80 // of an element an index
81 int smallest = index;
82
83 // If the left child is smaller than this element, it is
84 // the smallest
85 if (left < heap->size && heap->arr[left] < heap->arr[index])
86 smallest = left;
87
88 // Similarly for the right, but we are updating the smallest element
89 // so that it will definitely give the least element of the subtree
90 if (right < heap->size && heap->arr[right] < heap->arr[smallest])
91 smallest = right;
92
93 // Now if the current element is not the smallest,
94 // swap with the current element. The min heap property
95 // is now satisfied for this subtree. We now need to
96 // recursively keep doing this until we reach the root node,
97 // the point at which there will be no change!
98 if (smallest != index)
99 {
100 int temp = heap->arr[index];
101 heap->arr[index] = heap->arr[smallest];
102 heap->arr[smallest] = temp;
103 heap = heapify(heap, smallest);
104 }
105
106 return heap;
107}
108
109MinHeap* delete_minimum(MinHeap* heap) {
110 // Deletes the minimum element, at the root
111 if (!heap || heap->size == 0)
112 return heap;
113
114 int size = heap->size;
115 int last_element = heap->arr[size-1];
116
117 // Update root value with the last element
118 heap->arr[0] = last_element;
119
120 // Now remove the last element, by decreasing the size
121 heap->size--;
122 size--;
123
124 // We need to call heapify(), to maintain the min-heap
125 // property
126 heap = heapify(heap, 0);
127 return heap;
128}
129
130MinHeap* delete_element(MinHeap* heap, int index) {
131 // Deletes an element, indexed by index
132 // Ensure that it's lesser than the current root
133 heap->arr[index] = get_min(heap) - 1;
134
135 // Now keep swapping, until we update the tree
136 int curr = index;
137 while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
138 int temp = heap->arr[parent(curr)];
139 heap->arr[parent(curr)] = heap->arr[curr];
140 heap->arr[curr] = temp;
141 curr = parent(curr);
142 }
143
144 // Now simply delete the minimum element
145 heap = delete_minimum(heap);
146 return heap;
147}
148
149void print_heap(MinHeap* heap) {
150 // Simply print the array. This is an
151 // inorder traversal of the tree
152 printf("Min Heap:\n");
153 for (int i=0; i<heap->size; i++) {
154 printf("%d -> ", heap->arr[i]);
155 }
156 printf("\n");
157}
158
159void free_minheap(MinHeap* heap) {
160 if (!heap)
161 return;
162 free(heap->arr);
163 free(heap);
164}
165
166int main() {
167 // Capacity of 10 elements
168 MinHeap* heap = init_minheap(10);
169
170 insert_minheap(heap, 40);
171 insert_minheap(heap, 50);
172 insert_minheap(heap, 5);
173 print_heap(heap);
174
175 // Delete the heap->arr[1] (50)
176 delete_element(heap, 1);
177
178 print_heap(heap);
179 free_minheap(heap);
180 return 0;
181}
出发点( )
1Min Heap:
25 -> 50 -> 40 ->
3Min Heap:
45 -> 40 ->
实施时间的复杂性
上述程序的时间复杂性如下所述:
| Function | Time Complexity |
get_min() | O(1) |
insert_minheap() | O(logN) |
delete_minimum() | Same as insert - O(logN) |
heapify() | O(logN) |
delete_element() | O(logN) |
下载代码
你可以下载完整的代码作为我上传的 Github Gist 如果你有任何问题,请在下面的评论部分询问他们!
结论
在本文中,我们了解了如何代表一棵 Min Heap 二进制树,也看到了 C 中的实现。