合并排序是最有效的排序算法之一,它基于 Divide and Conquer的原则工作,基于将列表分解为多个子列表,直到每个子列表由一个单一的元素组成,并将这些子列表合并成一个排序列表。
混合型工作规则
分割和征服的概念包括三个步骤:
1、把问题分成多个子问题 2、解决子问题 2、把问题分解成原子子子问题 3、把子问题的解决方案结合起来,找到实际问题的解决方案
因此, merge 排序工作规则涉及以下步骤:
- 将未分类的数组分为子数组,每组都包含一个单元素
- 取两个单元素数组的邻近对,并将它们合并成一个由 2 个元素组成的数组
- 重复过程,直到获得单个分类的数组
一个大小N的数组被分为两部分的N/2大小,然后这些数组被进一步分割,直到我们达到一个单一的元素. 这里的基层案例达到一个单一的元素. 当基层案例被击中时,我们开始合并左部分和右部分,我们得到一个分类数组在末尾。 合并数组反复将一个数组分割成几个子数组,直到每个子数组由一个单一的元素组成,并合并这些子数组以一种结果的分类数组。
合并 Sort Algorithm Flow
Array = {70,50,30,10,20,40,60}
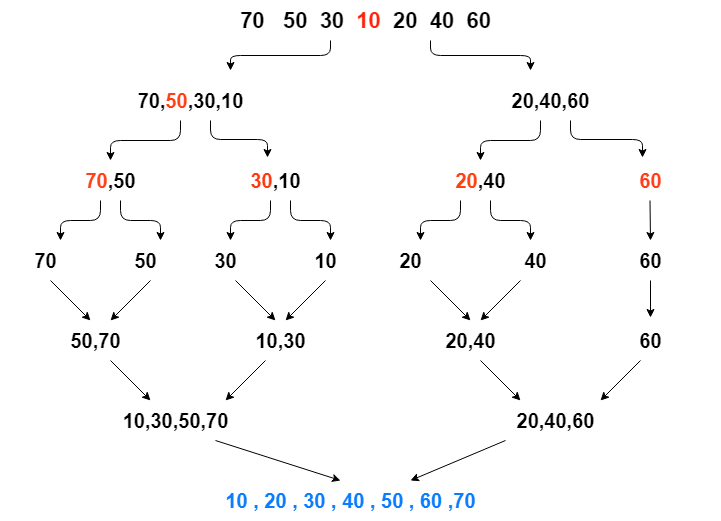
我们重复地把数组分成两部分,左部分和右部分,从中间元素进行分割,直到我们达到一个元素,然后我们开始将它们合并成一个分类数组。
混合类型实施
我们将在Java、C和Python中实施合并排序算法。
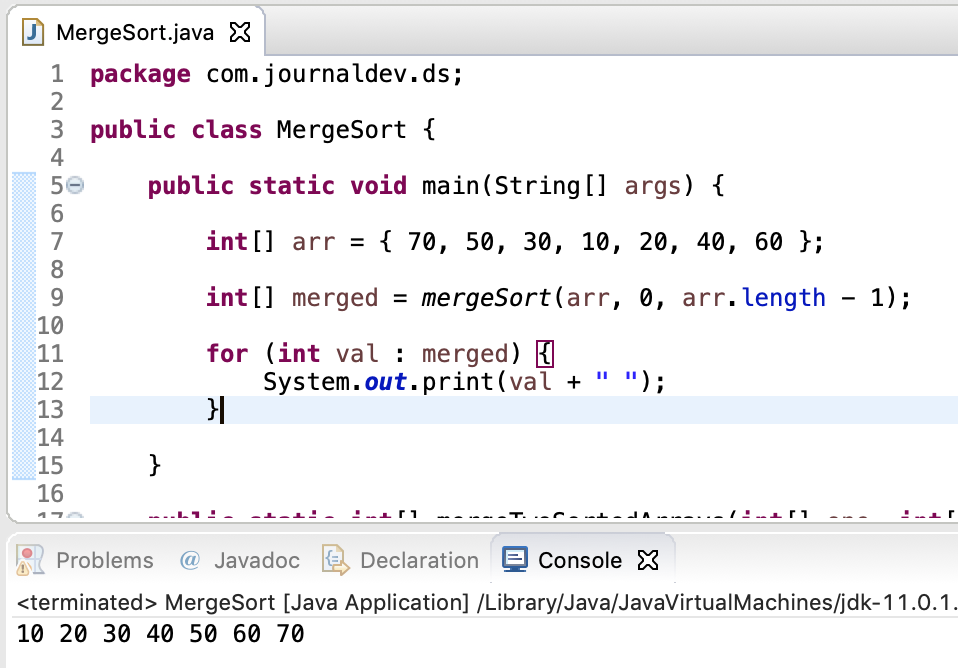
1、 Java 应用程序
1package com.journaldev.ds;
2
3public class MergeSort {
4
5 public static void main(String[] args) {
6
7 int[] arr = { 70, 50, 30, 10, 20, 40, 60 };
8
9 int[] merged = mergeSort(arr, 0, arr.length - 1);
10
11 for (int val : merged) {
12 System.out.print(val + " ");
13 }
14
15 }
16
17 public static int[] mergeTwoSortedArrays(int[] one, int[] two) {
18
19 int[] sorted = new int[one.length + two.length];
20
21 int i = 0;
22 int j = 0;
23 int k = 0;
24
25 while (i < one.length && j < two.length) {
26
27 if (one[i] < two[j]) {
28 sorted[k] = one[i];
29 k++;
30 i++;
31 } else {
32 sorted[k] = two[j];
33 k++;
34 j++;
35 }
36 }
37
38 if (i == one.length) {
39
40 while (j < two.length) {
41 sorted[k] = two[j];
42 k++;
43 j++;
44 }
45 }
46
47 if (j == two.length) {
48
49 while (i < one.length) {
50 sorted[k] = one[i];
51 k++;
52 i++;
53 }
54 }
55
56 return sorted;
57
58 }
59
60 public static int[] mergeSort(int[] arr, int lo, int hi) {
61
62 if (lo == hi) {
63 int[] br = new int[1];
64 br[0] = arr[lo];
65
66 return br;
67 }
68
69 int mid = (lo + hi) / 2;
70
71 int[] fh = mergeSort(arr, lo, mid);
72 int[] sh = mergeSort(arr, mid + 1, hi);
73
74 int[] merged = mergeTwoSortedArrays(fh, sh);
75
76 return merged;
77 }
78
79}
出发点( )
C 实施
1#include <stdio.h>
2
3void merge(int arr[], int l, int m, int r)
4{
5 int i, j, k;
6 int n1 = m - l + 1;
7 int n2 = r - m;
8
9 /* create temp arrays */
10 int L[n1], R[n2];
11
12 /* Copy data to temp arrays L[] and R[] */
13 for (i = 0; i < n1; i++)
14 L[i] = arr[l + i];
15 for (j = 0; j < n2; j++)
16 R[j] = arr[m + 1+ j];
17
18 /* Merge the temp arrays back into arr[l..r]*/
19 i = 0; // Initial index of first subarray
20 j = 0; // Initial index of second subarray
21 k = l; // Initial index of merged subarray
22 while (i < n1 && j < n2)
23 {
24 if (L[i] <= R[j])
25 {
26 arr[k] = L[i];
27 i++;
28 }
29 else
30 {
31 arr[k] = R[j];
32 j++;
33 }
34 k++;
35 }
36
37 /* Copy the remaining elements of L[], if there
38 are any */
39 while (i < n1)
40 {
41 arr[k] = L[i];
42 i++;
43 k++;
44 }
45
46 /* Copy the remaining elements of R[], if there
47 are any */
48 while (j < n2)
49 {
50 arr[k] = R[j];
51 j++;
52 k++;
53 }
54}
55
56/* l is for left index and r is the right index of the
57 sub-array of arr to be sorted */
58void mergeSort(int arr[], int l, int r)
59{
60 if (l < r)
61 {
62 // Same as (l+r)/2, but avoids overflow for
63 // large l and h
64 int m = l+(r-l)/2;
65
66 // Sort first and second halves
67 mergeSort(arr, l, m);
68 mergeSort(arr, m+1, r);
69
70 merge(arr, l, m, r);
71 }
72}
73
74void printArray(int A[], int size)
75{
76 int i;
77 for (i=0; i < size; i++)
78 printf("%d ", A[i]);
79 printf("\n");
80}
81
82/* Driver program to test above functions */
83int main()
84{
85 int arr[] = {70, 50, 30, 10, 20, 40,60};
86 int arr_size = sizeof(arr)/sizeof(arr[0]);
87
88 printf("Given array is \n");
89 printArray(arr, arr_size);
90
91 mergeSort(arr, 0, arr_size - 1);
92
93 printf("\nSorted array is \n");
94 printArray(arr, arr_size);
95 return 0;
96}
出发点( )
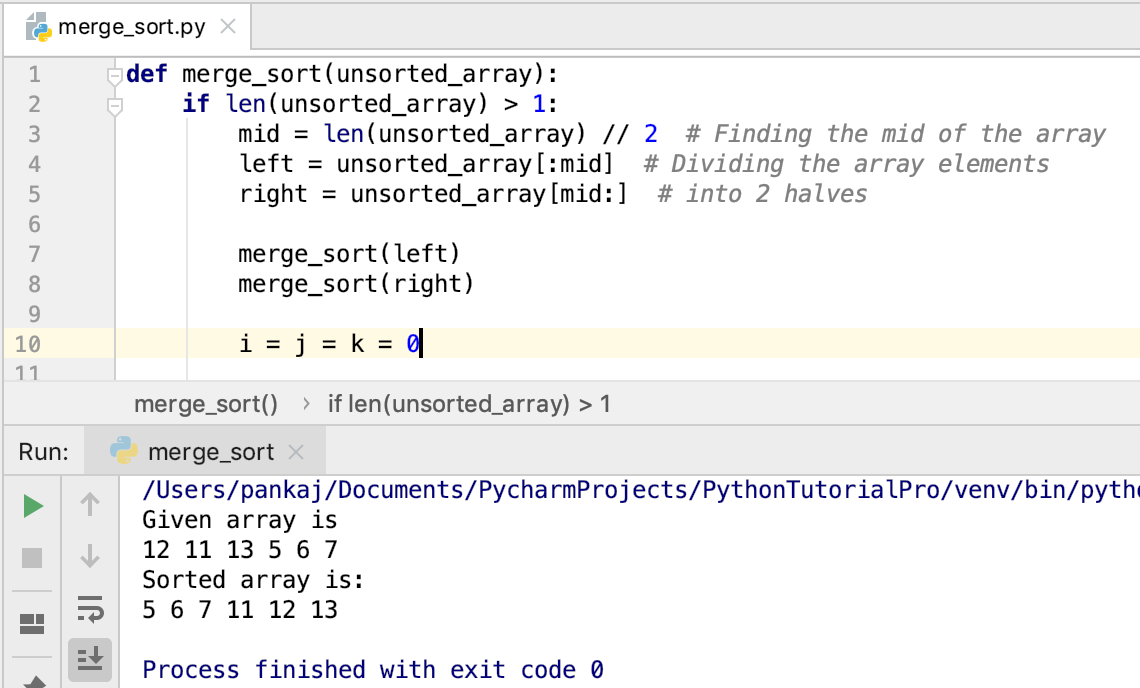
3、Python的应用
1def merge_sort(unsorted_array):
2 if len(unsorted_array) > 1:
3 mid = len(unsorted_array) // 2 # Finding the mid of the array
4 left = unsorted_array[:mid] # Dividing the array elements
5 right = unsorted_array[mid:] # into 2 halves
6
7 merge_sort(left)
8 merge_sort(right)
9
10 i = j = k = 0
11
12 # data to temp arrays L[] and R[]
13 while i < len(left) and j < len(right):
14 if left[i] < right[j]:
15 unsorted_array[k] = left[i]
16 i += 1
17 else:
18 unsorted_array[k] = right[j]
19 j += 1
20 k += 1
21
22 # Checking if any element was left
23 while i < len(left):
24 unsorted_array[k] = left[i]
25 i += 1
26 k += 1
27
28 while j < len(right):
29 unsorted_array[k] = right[j]
30 j += 1
31 k += 1
32
33# Code to print the list
34def print_list(array1):
35 for i in range(len(array1)):
36 print(array1[i], end=" ")
37 print()
38
39# driver code to test the above code
40if __name__ == '__main__':
41 array = [12, 11, 13, 5, 6, 7]
42 print("Given array is", end="\n")
43 print_list(array)
44 merge_sort(array)
45 print("Sorted array is: ", end="\n")
46 print_list(array)
出发点( )
合并 排序时间和空间复杂性
1、空间复杂性
辅助空间: O(n) 排序在位置: 没有算法 : ** 划分和征服**
2、时间复杂性
T(n) = 2T(n/2) + O(n)** 上述重复的解决方案是 O(nlog n). 尺寸N列表被划分为最多Logn部分,并将所有子列表合并成一个单一列表需要O(nlog n)时间,这个算法的最糟糕的运行时间是O(nLogn)最佳案例时间复杂性: **O(nlog n)**最糟糕的案例时间复杂性: **O(nlog n)**平均时间复杂性: O(nlog n) MergeSort的时间复杂性在所有3个案例中都是O(nLog n)(最糟糕,平均和最佳),因为合并总是将数组划分成两半线,并需要时间合并两半。