Level Order Traversal是穿越二进制树的一种方法,在本文中,我们将研究如何在C/C++中实现这个算法。
但在此之前,让我们把我们的概念涵盖起来。
构建概念
二进制树是一个数据结构,每个节点最多有两个孩子。
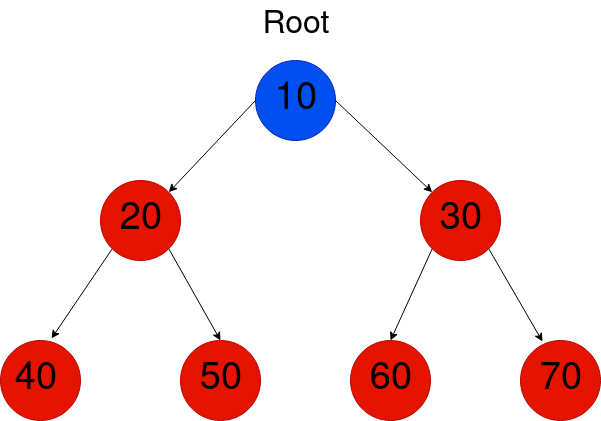
有四种常见的方式来穿越二进制树的节点,即:
- In order Traversal
- Pre Order Traversal
- Post Order Traversal
- Level Order Traversal
让我们来了解一个二进制树中的 ** 级别意味着什么。
一个层次是与树的某个节点相应的父母节点的数量,它基本上是从那个节点到根节点的祖先的数量。
因此,对于根节点(顶部节点),它的水平是0,因为它没有父母,如果它有孩子,两者都将有1级,因为它只有一个祖先,直到根节点,即根节点本身。
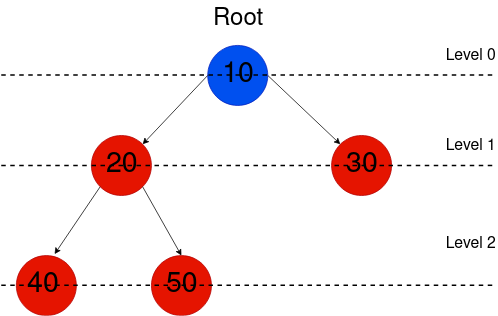
我们还需要理解二进制树中的高度( / 社区 / 教程 / 二进制树-in-c-plus)的概念,这只是从根到树中最深的节点的路径长度。
在这种情况下,高度将是从最深的节点(40或50,因为它们有最大水平)到根的长度。
现在我们已经涵盖了我们的概念,让我们来了解如何实现水平订单跨越。
级别 顺序 转移
一个 ** 级别顺序穿越 ** 是根据树的水平总是穿越的穿越。
因此,这条路径首先从根节点穿过对应于0级的节点,然后是1级,等等。
在上面的二进制树示例中,层次订单穿越将是:
(根) 10 -> 20 -> 30 -> 40 -> 50
为了做到这一点,我们需要做两件事。
我们必须首先找到树的高度 2 我们需要找到一个方法来打印与每个层面的节点
找出树木的高度
我們會先找出樹的高度,要做到這一點,邏輯很簡單。
由于树的高度被定义为从根到叶子的最大路径,所以我们可以反复计算左侧和右侧子树的高度,并找到子树的最大高度。
C类伪代码:
1// Find height of a tree, defined by the root node
2int tree_height(Node* root) {
3 if (root == NULL)
4 return 0;
5 else {
6 // Find the height of left, right subtrees
7 left_height = tree_height(root->left);
8 right_height = tree_height(root->right);
9
10 // Find max(subtree_height) + 1 to get the height of the tree
11 return max(left_height, right_height) + 1;
12}
打印每个级别的所有节点
现在我们有高度,我们必须为每个级别打印节点. 要做到这一点,我们将使用一个为循环重复所有级别到高度,并在每个级别打印节点。
1void print_tree_level_order(Node* root) {
2 int height = tree_height(root);
3 for (int i=0; i<height; i++) {
4 // Print the ith level
5 print_level(root, i);
6 }
7}
注意,我们需要另一个函数来打印树的i级别。
但是这一次,在打印根节点后,我们将根节点更改为它的左和右孩子,并打印两个子树。
这将继续,直到我们达到一个叶节点,也就是说,在下一步的辅助根将是NULL(因为 leaf_node->left =NULL和 leaf_node->right =NULL)
1void print_level(Node* root, int level_no) {
2 // Prints the nodes in the tree
3 // having a level = level_no
4
5 // We have a auxiliary root node
6 // for printing the root of every
7 // sub-tree
8 if (!root)
9 return;
10 if (level_no == 0) {
11 // We are at the top of a sub-tree
12 // So print the auxiliary root node
13 printf("%d -> ", root->value);
14 }
15 else {
16 // Make the auxiliary root node to
17 // be the left and right nodes for
18 // the sub-trees and decrease level by 1, since
19 // you are moving from top to bottom
20 print_level(root->left, level_no - 1);
21 print_level(root->right, level_no - 1);
22 }
23
24}
现在,我们终于完成了Level Order Traversal!
我将提供下面的完整程序,该程序还包括使用插入构建二进制树的部分。
完整的 C/C++ 代码
虽然这最初是一个C程序,但它也可以在C++上编译。
1/**
2 Code for https://journaldev.com
3 File Name: level_order.c
4 Purpose: Find the Level Order Traversal of a Binary Tree
5
6 @author Vijay Ramachandran
7 @date 28/01/2020
8*/
9
10#include <stdio.h>
11#include <stdlib.h>
12
13typedef struct Node Node;
14
15// Define the Tree Node here
16struct Node {
17 int value;
18 // Pointers to the left and right children
19 Node* left, *right;
20};
21
22Node* init_tree(int data) {
23 // Creates the tree and returns the
24 // root node
25 Node* root = (Node*) malloc (sizeof(Node));
26 root->left = root->right = NULL;
27 root->value = data;
28 return root;
29}
30
31Node* create_node(int data) {
32 // Creates a new node
33 Node* node = (Node*) malloc (sizeof(Node));
34 node->value = data;
35 node->left = node->right = NULL;
36 return node;
37}
38
39void free_tree(Node* root) {
40 // Deallocates memory corresponding
41 // to every node in the tree.
42 Node* temp = root;
43 if (!temp)
44 return;
45 free_tree(temp->left);
46 free_tree(temp->right);
47 if (!temp->left && !temp->right) {
48 free(temp);
49 return;
50 }
51}
52
53int tree_height(Node* root) {
54 // Get the height of the tree
55 if (!root)
56 return 0;
57 else {
58 // Find the height of both subtrees
59 // and use the larger one
60 int left_height = tree_height(root->left);
61 int right_height = tree_height(root->right);
62 if (left_height >= right_height)
63 return left_height + 1;
64 else
65 return right_height + 1;
66 }
67}
68
69void print_level(Node* root, int level_no) {
70 // Prints the nodes in the tree
71 // having a level = level_no
72
73 // We have a auxiliary root node
74 // for printing the root of every
75 // subtree
76 if (!root)
77 return;
78 if (level_no == 0) {
79 // We are at the top of a subtree
80 // So print the auxiliary root node
81 printf("%d -> ", root->value);
82 }
83 else {
84 // Make the auxiliary root node to
85 // be the left and right nodes for
86 // the subtrees and decrease level by 1, since
87 // you are moving from top to bottom
88 print_level(root->left, level_no - 1);
89 print_level(root->right, level_no - 1);
90 }
91
92}
93
94void print_tree_level_order(Node* root) {
95 if (!root)
96 return;
97 int height = tree_height(root);
98 for (int i=0; i<height; i++) {
99 printf("Level %d: ", i);
100 print_level(root, i);
101 printf("\n");
102 }
103 printf("\n\n-----Complete Level Order Traversal:-----\n");
104 for (int i=0; i<height; i++) {
105 print_level(root, i);
106 }
107 printf("\n");
108}
109
110int main() {
111 // Program to demonstrate Level Order Traversal
112
113 // Create the root node having a value of 10
114 Node* root = init_tree(10);
115
116 // Insert nodes onto the tree
117 root->left = create_node(20);
118 root->right = create_node(30);
119 root->left->left = create_node(40);
120 root->left->right = create_node(50);
121
122 // Level Order Traversal
123 print_tree_level_order(root);
124
125 // Free the tree!
126 free_tree(root);
127 return 0;
128}
出发点( )
1Level 0: 10 ->
2Level 1: 20 -> 30 ->
3Level 2: 40 -> 50 ->
4
5-----Complete Level Order Traversal:-----
610 -> 20 -> 30 -> 40 -> 50 ->
你也可以通过我为此创建的 Github gist下载。
结论
希望您能够更好地了解如何在 C/C++ 中实现 Level Order Traversal. 如果您有任何问题,请在下面的评论部分询问它们!