树木基本上只是精彩的 链接列表,树上创建和删除节点是令人难以置信的简单。
前提条件
我們的特殊例子是使用二進制搜索樹,但這些是更多的技術和模式,而不是精確的實施,可以很容易地適應任何類型的樹。
概念
使用 二进制搜索树我们可以使用相同的系统来创建一个新节点,以寻找一个. 标准树,像你的文件系统,不遵循任何特定的规则,并迫使我们通过树或子树查看每个项目,以找到我们想要的东西。
没有很多方法来优化过去的O(n)但有两个主要的哲学来搜索整个树,无论是通过搜索宽度第一(横向之间兄弟姐妹)或深度第一(垂直之间父母和孩子)。
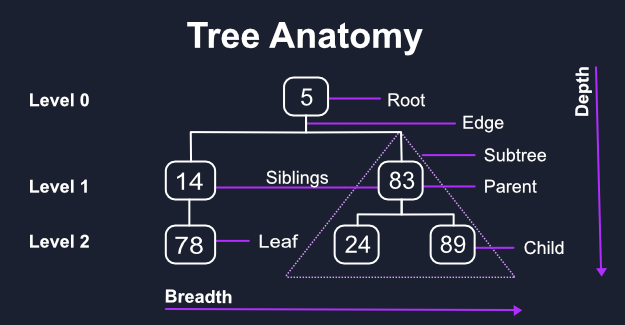
树
由于二进制搜索树是最容易设置的,我们可以简单地将一个快速的树组合起来,它只能添加节点。
1class Node {
2 constructor(val) {
3 this.val = val;
4 this.right = null;
5 this.left = null;
6 };
7};
8
9class BST {
10 constructor() {
11 this.root = null;
12 };
13 create(val) {
14 const newNode = new Node(val);
15 if (!this.root) {
16 this.root = newNode;
17 return this;
18 };
19 let current = this.root;
20
21 const addSide = side => {
22 if (!current[side]) {
23 current[side] = newNode;
24 return this;
25 };
26 current = current[side];
27 };
28
29 while (true) {
30 if (val === current.val) return this;
31 if (val < current.val) addSide('left');
32 else addSide('right');
33 };
34 };
35};
36
37const tree = new BST();
38tree.create(20);
39tree.create(14);
40tree.create(57);
41tree.create(9);
42tree.create(19);
43tree.create(31);
44tree.create(62);
45tree.create(3);
46tree.create(11);
47tree.create(72);
首页 > 搜索
宽度第一搜索的特点是,它专注于每一个项目,从左到右,在移动到下一个每个级别。
有三个主要部分,当前节点,我们访问的节点列表,以及一个基本的(https://andsky.com/tech/tutorials/js-stacks-queues)来跟踪我们需要查看的节点(我们只会使用一个数组,因为它永远不会很长)。
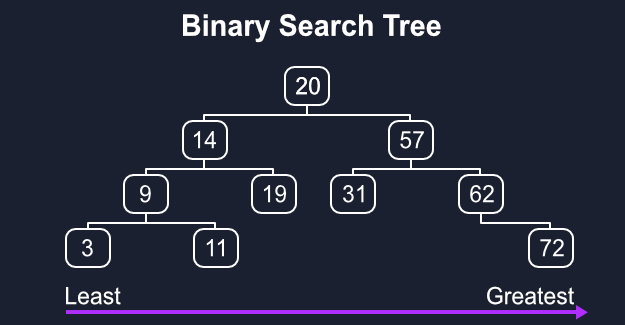
让我们来看看这棵树的样子。
无论我们的当前是什么,我们都会把它的孩子(从左到右)推入我们的队列,这样它就会看起来像[20, 14, 57]。
我们的当前项目现在可以删除并添加到访问,而我们继续到下一个项目,寻找其子女,并将其添加到排队,直到我们的排队是空的,每个值都在访问。
1BFS() {
2 let visited = [],
3 queue = [],
4 current = this.root;
5
6 queue.push(current);
7 while (queue.length) {
8 current = queue.shift();
9 visited.push(current.val);
10
11 if (current.left) queue.push(current.left);
12 if (current.right) queue.push(current.right);
13 };
14
15 return visited;
16}
17
18console.log(tree.BFS()); //[ 20, 14, 57, 9, 19, 31, 62, 3, 11, 72 ]
深度第一搜索
深度第一搜索比完成每一个层次更关心完成一道穿越树的整个侧面到叶子。
有三个主要方法来处理这一点,预订、邮购和订购,但它们只是彼此的很小的修改,以改变输出顺序。
从根开始,我们将使用一个短的 回归函数来记录我们的节点,然后移动到左边,尽可能地记录其路径。
1preOrder() {
2 let visited = [],
3 current = this.root;
4
5 let traverse = node => {
6 visited.push(node.val);
7 if (node.left) traverse(node.left);
8 if (node.right) traverse(node.right);
9 };
10
11 traverse(current);
12 return visited;
13}
14
15console.log(tree.preOrder()); // [ 20, 14, 9, 3, 11, 19, 57, 31, 62, 72 ]
正如你可能已经猜到的那样,邮寄是预订的反面,我们仍然在垂直工作,但不是从根到叶子,我们会从底部到顶部搜索。
我们将从最底部的左节点开始,并登录它及其兄弟姐妹,然后移动到他们的父母那里。
我们可以轻松地通过将我们的节点推到访问后,两条通道都完成。
1postOrder() {
2 let visited = [],
3 current = this.root;
4
5 let traverse = node => {
6 if (node.left) traverse(node.left);
7 if (node.right) traverse(node.right);
8 visited.push(node.val);
9 };
10
11 traverse(current);
12 return visited;
13}
14
15console.log(tree.postOrder()); // [ 3, 11, 9, 19, 14, 31, 72, 62, 57, 20 ]
类似于邮寄,预订访问从底部起作用,但它只是在任何兄弟姐妹之前访问父母。
而不是开始或结束,我们可以推到我们的列表后,我们穿过左边和右边之前. 我们的结果将看起来像这样的, [3, 9, 11, 14, 19, 20,...]。
1inOrder() {
2 let visited = [],
3 current = this.root;
4
5 let traverse = node => {
6 if (node.left) traverse(node.left);
7 visited.push(node.val);
8 if (node.right) traverse(node.right);
9 };
10
11 traverse(current);
12 return visited;
13}
14
15console.log(tree.inOrder()); // [ 3, 9, 11, 14, 19, 20, 31, 57, 62, 72 ]
关闭思想
当然,所有这些算法都将是O(n),因为重点是查看每个节点,没有太多的空间来切割角落或聪明的技巧。
请记住,这些不是需要记忆的确切实现,而是解决问题和构建更有价值的算法的一般模式。