由于基于比较的排序的性质,在数学上不可能改进远远超出O(nlogn)的范围,比如合并排序(https://andsky.com/tech/tutorials/js-understanding-merge-sort)和快速排序(https://andsky.com/tech/tutorials/js-quick-sort)。
前提条件
对 Big O Notation的基本理解对于与其他算法相比,思考radix sort 至关重要。
概念
Radix sort,也被称为bucket sort,是最古老的分类算法之一,甚至是早期存在的计算机。
它基于对我们需要比较的每个数据类型的子数组或桶的想法,例如A-Z或在我们的例子中0-9.我们在每个项目中采取第一个字符 / 数字,将整个项目添加到相应的桶中,然后将它们放回一个数组,同时保持新的顺序。
然后我们可以转到下一个字符 / 数字并重复过程. 当一个项目没有字符 / 数字时,我们会将其添加到第一个桶中,因为其他一切显然更大 / 更长。
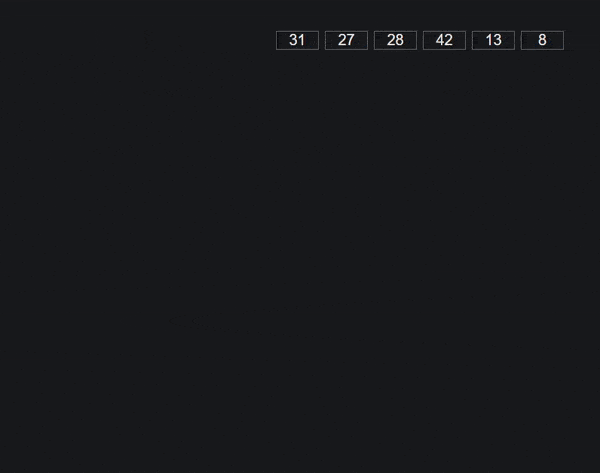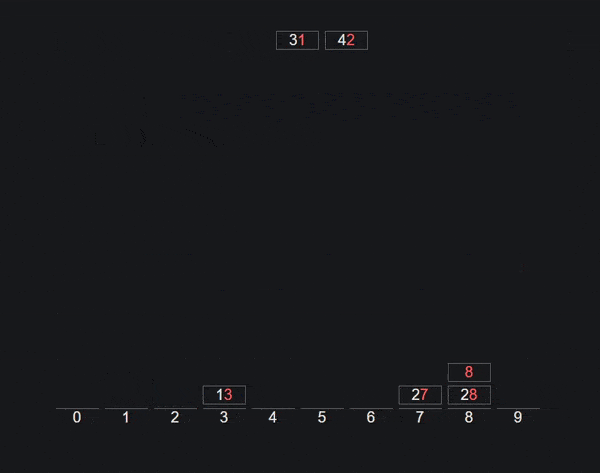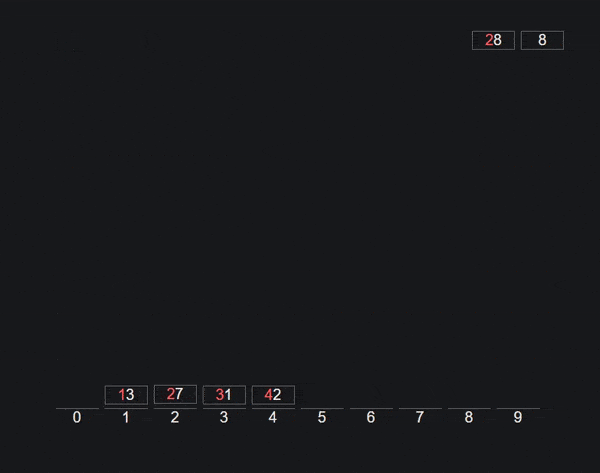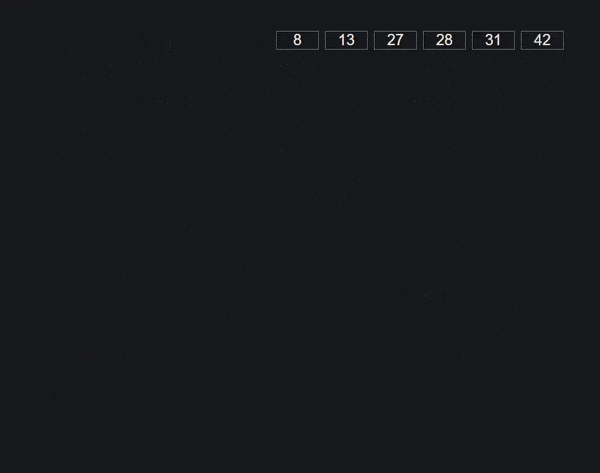
图形 / 动画 通过 VisuAlgo.net
实践数据
由于数字更简单,我们可以练习从1到50的数组。
1const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];
用途
由于我们正在使用数字,我们希望从最小的数字开始,然后工作起来,所以我们需要一种方法来从右边获得每个数字的索引。
我发现的最直观的方法是采取我们想要的数字,将其转换为一个字符串,并从中选择一个负索引的数组. 如果一个数字不在该索引中,我们可以返回一个零,所以它将被放置在我们排序的数组的前面。
1const getNum = (num, index) => {
2 const strNum = String(num);
3 let end = strNum.length - 1;
4 const foundNum = strNum[end - index];
5
6 if (foundNum === undefined) return 0;
7 else return foundNum;
8};
9
10console.log(getNum(4353, 2));
因为我们一次工作一次,我们需要算法来运行最长的数倍,所以如果我们有一个8位数的项目,它需要运行8次。
要找出它应该运行多少次,我们可以通过数组搜索最大的数字,然后返回其长度。
1const largestNum = arr => {
2 let largest = "0";
3
4 arr.forEach(num => {
5 const strNum = String(num);
6
7 if (strNum.length > largest.length) largest = strNum;
8 });
9
10 return largest.length;
11};
黑色 Radix
實施是相當直接的,為每個數位位置,我們可以使用「Array.from」來創建10個空的桶. 對於每個項目,他們將被放置在相應的桶中,當我們完成時,我們將把桶的數位整合成一個數位,從下一個字符位置開始。
1const radixSort = arr => {
2 let maxLength = largestNum(arr);
3
4 for (let i = 0; i < maxLength; i++) {
5 let buckets = Array.from({ length: 10 }, () => []);
6
7 for (let j = 0; j < arr.length; j++) {
8 let num = getNum(arr[j], i);
9
10 if (num !== undefined) buckets[num].push(arr[j]);
11 };
12 arr = buckets.flat();
13 };
14 return arr;
15};
16
17console.log(radixSort(unsortedArr));
结论
当我玩这个游戏时,我尝试了5000个项目,令我惊讶的是,它只用了23毫秒!我不知道你,但我认为这与我们迄今为止所涵盖的其他算法相比是一个令人难以置信的改进。