与 合并类型合作的一个问题是,他们需要在内存中创建和存储大量的数组,其中大部分是多余的数据。
前提条件
我们将讨论标准回归版本,尽管你可以重复地做到这一点,所以了解回归如何工作将是有帮助的,你可以在这里(https://andsky.com/tech/tutorials/js-understanding-recursion)刷。
概念
快速排序绝对是最不直观的算法之一,所以这里有一个非常简单的概述。
我们选择一个数字,称为我们的旋转,我们将将每一个数字与它进行比较,当我们通过我们的项目旋转时。目标是重新组织数组,以便它分为两半,每个项目中的每件事都小于或大于我们的旋转。
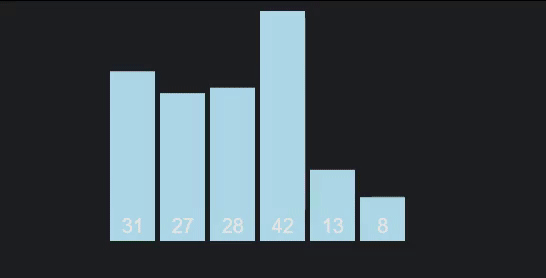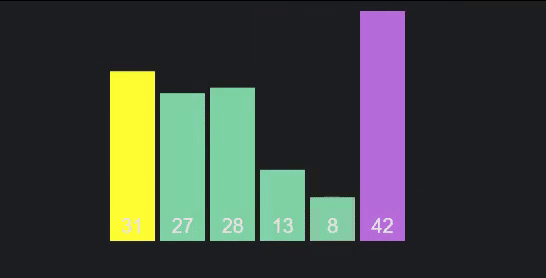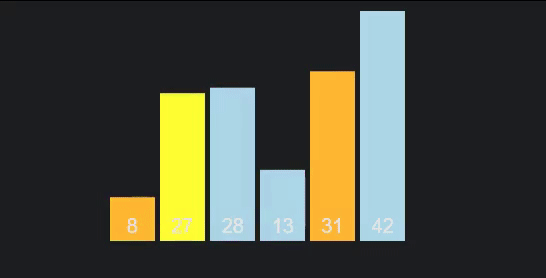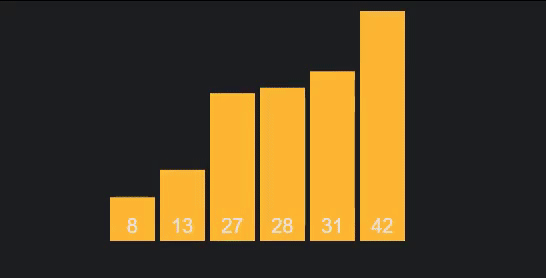
图形 / 动画 通过 VisuAlgo.net
就像 merge 类一样,平均复杂度为 O(nlogn),所以你选择哪个是你的选择。
实践数据
像往常一样,这里有一个50个随机数字的未分类数组,我还建议看看JavaScript的 性能 api以与其他算法和不同的数据进行比较。
1const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];
皮尔
首先,我们需要我们的旋转实用函数,有4个主要部分,我们的交换器,循环,旋转本身和我们的指针。
我们的指针仅仅是我们旋转的站点。每次我们的循环进展时,每个项目都与旋转进行比较,如果小,则与我们的旋转器进行交换。每次我们这样做,就是确保旋转器在比旋转更小的东西和更大的东西前面。当一切都完成了,我们的阵列被分割了,那么我们可以将旋转器分配给旋转器的索引作为其最终位置。
我们的交换工作只是将每个项目的索引重新分配到对方的索引中,没有什么太疯狂的。
1const pivot = (arr, start = 0, end = arr.length + 1) => {
2 const swap = (list, a, b) => [list[a], list[b]] = [list[b], list[a]];
3
4 let pivot = arr[start],
5 pointer = start;
6
7 for (let i = start; i < arr.length; i++) {
8 if (arr[i] < pivot ) {
9 pointer++;
10 swap(arr, pointer, i);
11 }
12 };
13 swap(arr, start, pointer);
14
15 return pointer;
16}
快速黑色
我们将使用我们的转函数从我们的数组中获取第一个分类项目. 这样,我们将重复运行我们的quickSort,在我们分割数组的第一半部分执行相同的过程,这将重复,直到没有剩下什么可分类,然后对另一半做同样的事情. 当两者完成时,我们的完全分类数组可以返回。
1const quickSort = (arr, start = 0, end = arr.length) => {
2 let pivotIndex = pivot(arr, start, end);
3
4 if (start >= end) return arr;
5 quickSort(arr, start, pivotIndex);
6 quickSort(arr, pivotIndex + 1, end);
7
8 return arr;
9};
10
11console.log(quickSort(unsortedArr));
结论
快速排序绝对是最困难的排序算法之一,把我的头包围起来。在有4个变更部分和2个回归堆栈之间,这绝对是你可能不应该期望完全记住的东西,并且可能想为以后的参考打字。