JavaScript 提供了一些非常方便的工具,可以通过数组搜索,但有了大数据集,O(n)方法如indexOf,find或基本循环只是不是最好的,甚至是可行的。
前提条件
我将使用Big O Notation来比较性能和复杂性,你可以在这里刷新(https://andsky.com/tech/tutorials/js-big-o-notation)。
实践数据
以下是一些分类和不分类的数据集,其中有50个项目,我将参考。
1const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];
2
3const sortedArr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50];
线性搜索
这是标准的 brute-force 解决方案,我相信你已经做过一千次了,我们只是说,我需要一些东西,所以一看一看,直到你找到它。
1const linear = (arr, target) => {
2 let steps = 0;
3
4 for (let i = 0; i < arr.length; i++) {
5 steps++;
6 if (arr[i] === target) return `Found: ${arr[i]} in ${steps} steps`;
7 };
8};
9
10console.log(linear(unsortedArr, 40)); // 40 steps in 40 Milliseconds
11console.log(linear(sortedArr, 40)); // 40 steps in 40 Milliseconds
二进制搜索
而不是浪费资源看数据,显然不是我们想要的,我们可以使用分割和征服方法,使每一个操作都集中在忽略我们不想要的东西,而不是痛苦地寻找我们想要的东西。
我们有三个主要组件,两个指针和一个旋转。每一个旋转开始于数组的两端,中间有旋转,然后我们检查我们想要的比我们的旋转高或低,如果高,那么左旋转将移动到旋转的位置,而旋转将移动到新的中间。
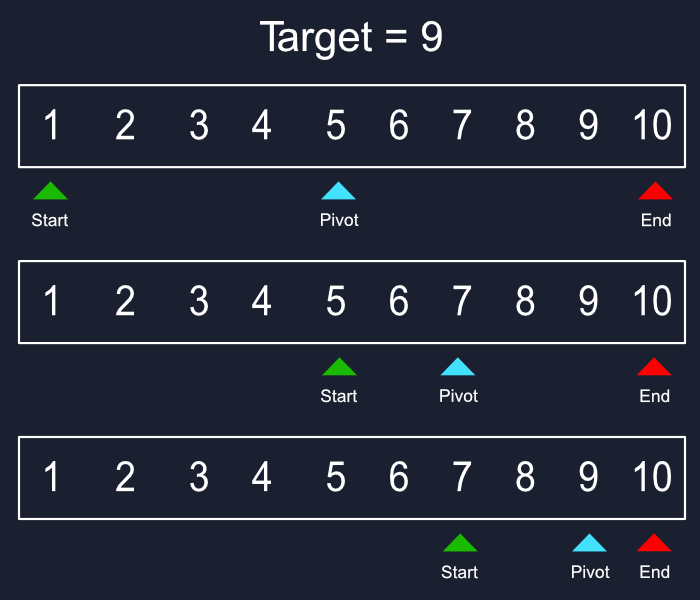
每一步,我们都在将数据集切成一半,完全忽略了我们不需要的东西,给了我们O(logn)的时间复杂性,如果我们在一百万个项目中搜索一个数字,需要十步,那么十亿个项目的搜索可能只需要15到20步。
1const binary = (arr, target) => {
2 let start = 0;
3 let end = arr.length;
4 let pivot = Math.floor((start + end) / 2);
5 let steps = 0;
6
7 for (let i = 0; i < arr.length; i++) {
8 if (arr[pivot] !== target) {
9 if (target < arr[pivot]) end = pivot;
10 else start = pivot;
11 pivot = Math.floor((start + end) / 2);
12 steps++;
13 };
14
15 if (arr[pivot] === target) return `Found: ${target} in ${steps} steps`;
16 };
17
18 return 'Nothing Found';
19};
20
21console.log(linear(unsortedArr, 40)); // Nothing Found
22console.log(binary(arr, 44)); // 5 steps in 8 Milliseconds
23console.log(binary(arr, 43)); // 2 steps in 7 Milliseconds
二进制搜索的主要缺点是,它只允许我们在排序的数组上做到这一点,但还有其他解决方案可以基于在搜索之前预先排序数据。
结论
这只是应用二进制搜索的一种方法,但这个想法可以重新配置用于各种数据结构,只要它是排序的,在未来,我希望我们可以利用这种技术来通过更先进的数据集以闪电的速度探索。