如果您在您的计算机上运行搜索文件,它通常需要很长时间,这是因为您的文件是未分类的,它必须搜索任何东西,以获得一个结果。
前提条件
你需要知道树木的基本概念,你可以学到这里(LINK0),我们还需要做一些非常基本的树木穿越与宽度第一搜索,你可以刷在这里(LINK1)。
概念
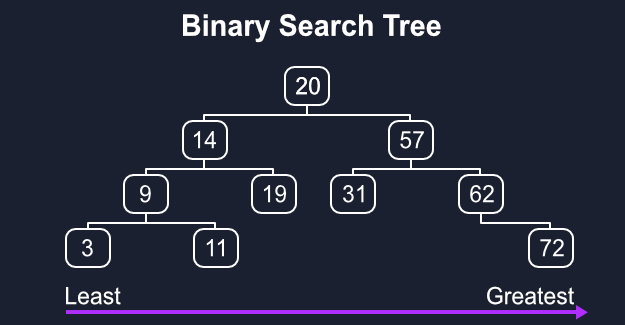
二进制搜索树只是一个正常的树,每个节点的局限性只能够,最多,有两个孩子. 二进制搜索树只是有一个额外的规则,如果有两个值,那么它们需要被排序,在我们的情况下,从左边的较低的数字到右边的较高。
在二进制搜索树上搜索是我们最初的O(n)搜索速度的一个重大改进,从现在开始,我们只需要比较我们想要的每一个母节点,然后移动到左或右,直到我们达到我们想要的速度,为所有操作提供O(logn)。
创造
非常类似于 链接列表我们可以使用类来生成我们的节点和树. 每个节点只需要向左 / 较低和较大 / 右侧的指针,值,我个人喜欢添加计数器,因为重复值只能存在一次在树上。
很简单,我们只需要循环通过树,如果我们的值小于当前节点移动左边其他移动右边,如果没有什么就成为新的节点在那个位置,如果一个匹配的值已经在那里,那么我们可以增加其计数器。
1class Node {
2 constructor(val) {
3 this.val = val;
4 this.right = null;
5 this.left = null;
6 this.count = 0;
7 };
8};
9
10class BST {
11 constructor() {
12 this.root = null;
13 }
14 create(val) {
15 const newNode = new Node(val);
16 if (!this.root) {
17 this.root = newNode;
18 return this;
19 };
20 let current = this.root;
21
22 const addSide = side => {
23 if (!current[side]) {
24 current[side] = newNode;
25 return this;
26 };
27 current = current[side];
28 };
29
30 while (true) {
31 if (val === current.val) {
32 current.count++;
33 return this;
34 };
35 if (val < current.val) addSide('left');
36 else addSide('right');
37 };
38 };
39};
40
41let tree = new BST();
42tree.add(10);
43tree.add(4);
44tree.add(4);
45tree.add(12);
46tree.add(2);
47console.log(tree);
找到
找到一些东西是非常简单的,只需向左或向右移动,相对当前值,如果我们击中匹配的东西,则返回真。
1find(val) {
2 if (!this.root) return undefined;
3 let current = this.root,
4 found = false;
5
6 while (current && !found) {
7 if (val < current.val) current = current.left;
8 else if (val > current.val) current = current.right;
9 else found = true;
10 };
11
12 if (!found) return 'Nothing Found!';
13 return current;
14};
删除
删除是最复杂的操作,因为我们不只使用叶子,而是需要重组或重新平衡一个节点的所有子女。
首先,我们需要一个实用功能来收集被删除节点的所有孩子,我会使用一个基本的宽度第一搜索,将一切推入一个数组,然后我们可以循环通过重新添加每一个项目到树上。
与正常搜索的唯一区别在于它需要接受不同的起点,所以我们只能将搜索限制在我们删除节点的子女的子树中。
1BFS(start) {
2 let data = [],
3 queue = [],
4 current = start ? this.find(start) : this.root;
5
6 queue.push(current);
7 while (queue.length) {
8 current = queue.shift();
9 data.push(current.val);
10
11 if (current.left) queue.push(current.left);
12 if (current.right) queue.push(current.right);
13 };
14
15 return data;
16}
由于我们无法回到父母,我们将使用变量将父母节点存储为当前,然后在我们保存孩子后使用它将当前设置为零。
在删除Node中,我们将收集我们的节点的孩子,将其设置为null,然后在每个孩子上使用创建,在树上正确重组它们。
1delete(val) {
2 if (!this.root) return undefined;
3 let current = this.root,
4 parent;
5
6 const pickSide = side => {
7 if (!current[side]) return 'No node found!';
8
9 parent = current;
10 current = current[side];
11 };
12
13 const deleteNode = side => {
14 if (current.val === val && current.count > 1) current.count--;
15 else if (current.val === val) {
16 const children = this.BFS(current.val);
17 parent[side] = null;
18 children.splice(0, 1);
19 children.forEach(child => this.create(child));
20 };
21 };
22
23 while (current.val !== val) {
24 if (val < current.val) {
25 pickSide('left');
26 deleteNode('left');
27 };
28 else {
29 pickSide('right');
30 deleteNode('right');
31 };
32 };
33
34 return current;
35}
结论
这将是完整的CRUD操作,因为任何更新基本上只是删除一个节点,并在其他地方创建一个全新的节点,这实际上不需要自己的方法。
我们将能够用二进制搜索树做一些更酷的事情,因为我们进入了二进制堆和优先排队。