虽然我确信我们可以都同意,尾巴(LINK0)是自切面包以来最酷的东西,但我们实际上可以通过将它们与一种叫做堆积的变种(LINK1)混合来做得更好。
概念
与 二进制搜索树不同,我们在兄弟之间比较和组织我们的价值观,在堆积中我们只在父母和他们的孩子之间工作,这给了我们两个堆积的可能性,即最大堆积和小堆积,无论您是从最高到最低的值,还是相反。
与二进制搜索树一样,二进制堆只允许一个父母有两个或更少的孩子,它们也是特殊的,因为它们总是平衡的,因为每一个新节点都将被添加到从左到右到完整的水平。
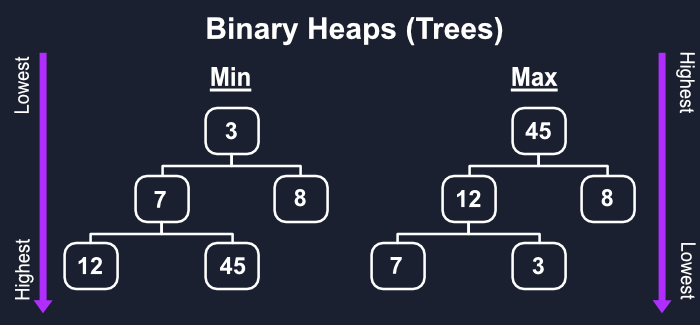
不幸的是,链接列表通常不是对二进制堆积的最佳方法,尽管通常被概念化为有左和右孩子的树,尽管仍然可以。
大多数时候,将更好地处理它作为一个阵列,所以这就是我们将在这里涵盖的。
通过这种方式,我们创建了一个非常一致的模式来找到一个节点的孩子.节点的所有左边的孩子将完全处于离他们的父母的位置2n + 1,而n是他们的父母的指数,所有正确的孩子则是2n + 2。
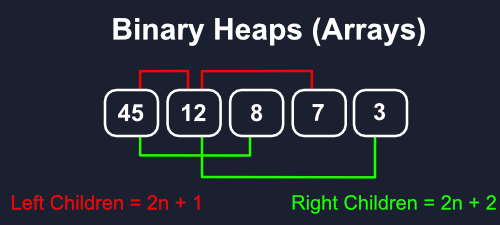
添加节点
似乎添加一个新的节点就像推到我们的数组一样简单,但复杂的部分是,我们需要将其与自己和max之间的父母进行比较,然后相应地重新排序它们。

图形 / 动画 通过 VisuAlgo.net
在我们将我们的新项目推到数组的尽头后,我们需要泡沫我们的更大的值,首先,我们需要抓住数组的尽头的新项目,我们将将其分解为索引和该索引的新项目。
每当我们添加一个项目时,我们将使用我们的方程式的反面来找到孩子, (n-1)/2,以找到其父母. 如果其父母小于当前节点,交换它们,然后保存其索引,这将是下一个‘当前’。
由于它将逐步从底部移动我们的指数,只要它大于零,继续交换。
1class BH {
2 constructor() {
3 this.values = [];
4 }
5 add(element) {
6 this.values.push(element);
7 let index = this.values.length - 1;
8 const current = this.values[index];
9
10 while (index > 0) {
11 let parentIndex = Math.floor((index - 1) / 2);
12 let parent = this.values[parentIndex];
13
14 if (parent <= current) {
15 this.values[parentIndex] = current;
16 this.values[index] = parent;
17 index = parentIndex;
18 } else break;
19 }
20 }
21}
22
23const tree = new BH();
24tree.add(3);
25tree.add(4);
26tree.add(31);
27tree.add(6);
28console.log(tree); // [31, 6, 4, 3]
删除 马克斯
我们将返回第一个节点,我们的max,然后采取最后一个节点,我们的数组的尽头,并将其设置为新的max。
我们这样做,以便我们可以使用我们的最低值作为一个容易的基准来与我们的其他值进行比较,因为我们沉没回到树底,同时在途中进行比较和交换。
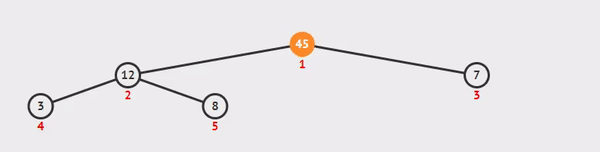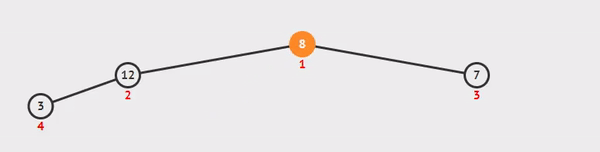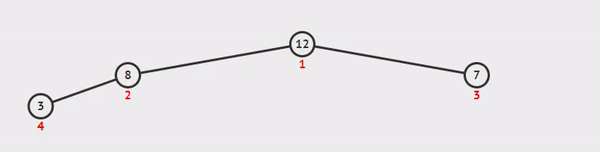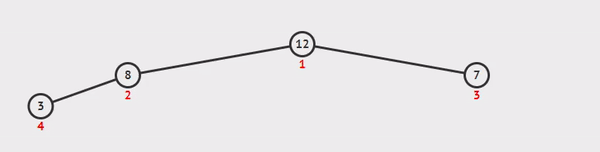
图形 / 动画 通过 VisuAlgo.net
简单的部分是抓住我们当前的最大值,然后在用最后一个项目取代之前取消它,然后我们可以在所有其他事情完成后返回我们的原始最大值。
一旦我们有一个起始索引,我们想要抓住它的右和左孩子. 如果左孩子是一个有效的项目,并且更大,那么我们可以将其保存为交换,在所有比较完成后运行交换。
正确的孩子有点复杂,我们只想要一个,而且最大的,孩子与父母交换. 我们将添加一个单独的要求,即rightChild只能被设置为swap,如果它尚未定义或大于leftChild。
1class BH {
2 extractMax() {
3 const max = this.values[0];
4 const end = this.values.pop();
5 this.values[0] = end;
6
7 let index = 0;
8 const length = this.values.length;
9 const current = this.values[0];
10 while (true) {
11 let leftChildIndex = 2 * index + 1;
12 let rightChildIndex = 2 * index + 2;
13 let leftChild, rightChild;
14 let swap = null;
15
16 if (leftChildIndex < length) {
17 leftChild = this.values[leftChildIndex];
18 if (leftChild > current) swap = leftChildIndex;
19 }
20 if (rightChildIndex < length) {
21 rightChild = this.values[rightChildIndex];
22 if (
23 (swap === null && rightChild > current) ||
24 (swap !== null && rightChild > leftChild)
25 )
26 swap = rightChildIndex;
27 }
28
29 if (swap === null) break;
30 this.values[index] = this.values[swap];
31 this.values[swap] = current;
32 index = swap;
33 }
34
35 return max;
36 }
37}
38
39const tree = new BH();
40tree.add(3);
41tree.add(4);
42tree.add(31);
43tree.add(6);
44console.log(tree.extractMax()); // 31
优先队列
通过一些小小的调整,我们可以将二进制堆栈与队列混合,并创建一个类型的队列,以重要性来组织我们的数据,而不是在添加时。
我们可以通过存储节点而不是单个数字来实现这一点,每个节点将有一个优先级级别(例如从1到5),它将用来确定顺序。
我们只需要使用节点的优先级每当我们在如果陈述中进行比较。
1class Node {
2 constructor(val, priority) {
3 this.val = val;
4 this.priority = priority;
5 }
6}
7
8class PQ {
9 constructor() {
10 this.values = [];
11 }
12 enqueue(val, priority) {
13 let newNode = new Node(val, priority);
14 this.values.push(newNode);
15 let index = this.values.length - 1;
16 const current = this.values[index];
17
18 while (index > 0) {
19 let parentIndex = Math.floor((index - 1) / 2);
20 let parent = this.values[parentIndex];
21
22 if (parent.priority <= current.priority) {
23 this.values[parentIndex] = current;
24 this.values[index] = parent;
25 index = parentIndex;
26 } else break;
27 }
28 }
29 dequeue() {
30 const max = this.values[0];
31 const end = this.values.pop();
32 this.values[0] = end;
33
34 let index = 0;
35 const length = this.values.length;
36 const current = this.values[0];
37 while (true) {
38 let leftChildIndex = 2 * index + 1;
39 let rightChildIndex = 2 * index + 2;
40 let leftChild, rightChild;
41 let swap = null;
42
43 if (leftChildIndex < length) {
44 leftChild = this.values[leftChildIndex];
45 if (leftChild.priority > current.priority) swap = leftChildIndex;
46 }
47 if (rightChildIndex < length) {
48 rightChild = this.values[rightChildIndex];
49 if (
50 (swap === null && rightChild.priority > current.priority) ||
51 (swap !== null && rightChild.priority > leftChild.priority)
52 )
53 swap = rightChildIndex;
54 }
55
56 if (swap === null) break;
57 this.values[index] = this.values[swap];
58 this.values[swap] = current;
59 index = swap;
60 }
61
62 return max;
63 }
64}
65
66const tree = new BH();
67tree.enqueue(3, 2);
68tree.enqueue(4, 5);
69tree.enqueue(31, 1);
70tree.enqueue(6, 3);
71console.log(tree.dequeue()); // 4
72console.log(tree.dequeue()); // 6
73console.log(tree.dequeue()); // 3
74console.log(tree.dequeue()); // 31
关闭思想
正如我们使用的标准队列一样,优先队列对于智能穿越图表和更复杂的结构至关重要。
将 max 堆积转换为 min 堆积就像我们所有比较中更改大于小于符号一样简单。