如果你曾经想过获得开发人员的工作,你可能在某个时候遇到这个(Google采访)(https://www.youtube.com/watch?v=XKu_SEDAykw)并想知道他们在谈论什么混蛋?在本文中,我们将探讨它们的含义,比如平方和n log n。
在这些例子中,我将参考这两个数组,一个有5个项目,另一个有50个项目,我也将使用JavaScript的实用性能API(https://andsky.com/tech/tutorials/js-js-performance-api)来衡量执行时间的差异。
1const smArr = [5, 3, 2, 35, 2];
2
3const bigArr = [5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2];
什么是Big O Notation?
虽然有其它符号,但O符号通常是最常用的,因为它专注于最坏的情况,这更容易量化和思考。最坏的情况意味着完成任务所需的操作最多;如果你在一秒钟内解决了鲁比克立方体,你不能说你是最好的,如果它只需要一圈才能完成。
随着您了解更多关于算法的信息,您将看到这些表达式被广泛使用,因为在理解这种关系时写代码可以是操作几乎即时或需要几分钟的时间和浪费,有时是巨额的,对外部处理器(如Firebase)的差异。
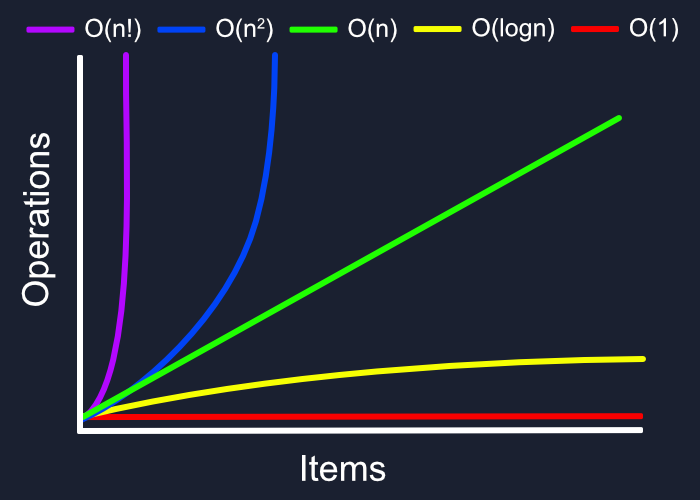
随着您了解更多关于大O符号的信息,您可能会看到这个图表的许多不同和更好的变异,我们希望保持我们的复杂性尽可能低和直,理想情况下避免O(n)以上的任何东西。
或(1)
這是理想的,無論有多少項目,無論是一個或一百萬,完成時間的數量將保持相同。 大多數執行單一操作的操作都是O(1).推到一個數列,得到一個項目在一個特定的索引,添加一個孩子元素,等等,都需要相同的時間,無論數列的長度。
1const a1 = performance.now();
2smArr.push(27);
3const a2 = performance.now();
4console.log(`Time: ${a2 - a1}`); // Less than 1 Millisecond
5
6const b1 = performance.now();
7bigArr.push(27);
8const b2 = performance.now();
9console.log(`Time: ${b2 - b1}`); // Less than 1 Millisecond
或(n)
默认情况下,所有循环都是线性增长的例子,因为数据大小和完成时间之间存在一个对一个的关系,因此,一个具有1000倍以上项目的数组将需要精确的1000倍的时间。
1const a1 = performance.now();
2smArr.forEach(item => console.log(item));
3const a2 = performance.now();
4console.log(`Time: ${a2 - a1}`); // 3 Milliseconds
5
6const b1 = performance.now();
7bigArr.forEach(item => console.log(item));
8const b2 = performance.now();
9console.log(`Time: ${b2 - b1}`); // 13 Milliseconds
O(n^2)
指數增長是一個陷阱,我們都至少有一次陷入了。 需要找到一個對應對象的每個項目在一個數列中? 把一個循環在一個循環內的一個循環是一個很好的方式,將一組1000個項目轉換成一百萬的操作搜索,這將凍結你的瀏覽器。
1const a1 = performance.now();
2smArr.forEach(() => {
3 arr2.forEach(item => console.log(item));
4});
5const a2 = performance.now();
6console.log(`Time: ${a2 - a1}`); // 8 Milliseconds
7
8const b1 = performance.now();
9bigArr.forEach(() => {
10 arr2.forEach(item => console.log(item));
11});
12const b2 = performance.now();
13console.log(`Time: ${b2 - b1}`); // 307 Milliseconds
O(日志 n)
我听说过的理解逻辑增长的最佳比喻是想象在字典中寻找一个像笔记这样的单词,你不能搜索一个单元,而是找到N部分,然后也许是OPQ页面,然后在字母中搜索列表,直到你找到一个匹配。
通过这种分割和征服方法,找到某些东西的时间量仍然会取决于字典的大小,但不会接近O(n)的速度,因为它在不查看大多数数据的情况下逐步搜索更具体的部分,通过一千个项目进行搜索可能需要不到10次操作,而一百万可能需要不到20次,让你获得最多的钱。
在这个例子中,我们可以做一个简单的 quicksort。
1const sort = arr => {
2 if (arr.length < 2) return arr;
3
4 let pivot = arr[0];
5 let left = [];
6 let right = [];
7
8 for (let i = 1, total = arr.length; i < total; i++) {
9 if (arr[i] < pivot) left.push(arr[i]);
10 else right.push(arr[i]);
11 };
12 return [
13 ...sort(left),
14 pivot,
15 ...sort(right)
16 ];
17};
1sort(smArr); // 0 Milliseconds
2sort(bigArr); // 1 Millisecond
O(n)
最后,最糟糕的可能性之一,因子增长. 教科书的例子是旅行卖家(https://en.wikipedia.org/wiki/Travelling_salesman_problem)的问题. 如果你有一个城市的堆积不同距离,你如何找到最短的路径,走在他们所有之间,返回起点? 粗力方法将是检查每个城市之间可能的配置之间的距离,这将是一个因子和快速脱离手。
由于这个问题变得非常复杂非常快,我们将用一个短的回归函数来证明这种复杂性。这个函数将以其自身的函数来倍增一个数字,以减去一个。我们因数中的每一个数字都会运行自己的函数,直到它达到0,每个回归层将其产品添加到我们的原始号码中。
<$>[注] 因数只是每个数字的产物,直到这个数字为止.所以6!是1x2x3x4x5x6 = 720. <$>
1const factorial = n => {
2 let num = n;
3
4 if (n === 0) return 1
5 for (let i = 0; i < n; i++) {
6 num = n * factorial(n - 1);
7 };
8
9 return num;
10};
1factorial(1); // 2 Milliseconds
2factorial(5); // 3 Milliseconds
3factorial(10); // 85 Milliseconds
4factorial(12); // 11,942 Milliseconds
我打算显示因数(15),但超过12的任何东西都太多了,并崩溃了页面,从而证明了为什么需要避免这一点。
关闭思想
保持你的代码尽可能的性能可能看起来像一个明显的担忧,但我相信几乎每个开发者都至少有一次创建了双重或甚至三重嵌套循环,因为它只是工作。