在本教程中，我们将讨论二叉树。我们将看到如何递归和迭代地计算树数据结构的高度。

二叉树

二叉树是一种数据结构，其中数据以分层方式存储，而不是线性存储(就像在LinkedList和数组中那样)。二叉树数据结构由节点组成。每个节点保存数据以及对子指针(左和右)的引用。二叉树的根是最上面的节点。(与真正活着的树截然相反)。下面是带有一些节点的树的插图。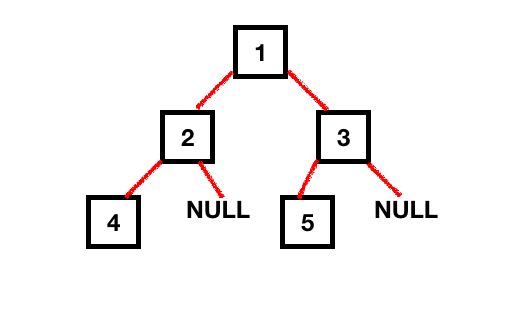节点的高度是从该节点到叶子的最长下行路径的长度。根的高度就是树的高度。因此，为了计算树的高度，我们需要遍历树的每个节点，以获得所有的排列和组合。有两种方法可以计算树的高度。

递归方式
迭代方式

树的高度-递归

递归包括计算子问题的结果并将其返回到父问题。

涉及的步骤 ：

1.要递归计算树的高度，需要递归地找出树的左子树和右子树的高度，并将其加1(最上面的节点与其子节点之间的高度)。 2.这些子树中的每个子树本身都可以有一个左子树和右子树，因此递归将一直应用到这些子树为空。空树节点的高度为-1。 3.最后，我们将比较左子树和右子树的高度，并返回较大的那个。

下面的插图显示了计算二叉树高度的排列数。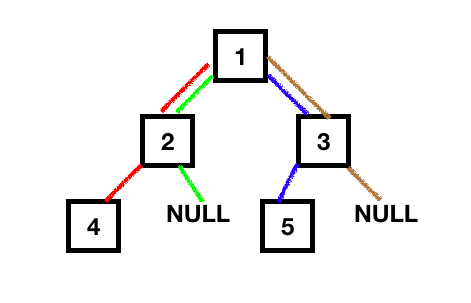让我们编写Java程序来递归计算树的高度。首先，我们将有一个树数据结构的基本实现。

 1package com.journaldev.tree.height;
 2
 3public class BinaryTree {
 4
 5    TreeNode root;
 6
 7    public static class TreeNode {
 8
 9    	TreeNode left;
10    	TreeNode right;
11    	Object data;
12
13    	TreeNode(Object data) {
14    		this.data = data;
15    		left = right = null;
16    	}
17    }
18}

让我们看一下使用递归查找树高度的代码。

 1package com.journaldev.tree.height;
 2
 3import com.journaldev.tree.height.BinaryTree.TreeNode;
 4
 5public class HeightOfTree {
 6
 7    public static void main(String[] args) {
 8
 9    	BinaryTree binaryTree = new BinaryTree();
10
11    	/**
12    	 * Binary Tree in our example, height = 2
13    	 * 		1		(Root)
14    	 * 	  2	  3		(Level 1)
15    	 *  4    	 5		(Level 2)
16    	 */
17    	binaryTree.root = new TreeNode(1);
18    	binaryTree.root.left = new TreeNode(2);
19    	binaryTree.root.right = new TreeNode(3);
20    	binaryTree.root.left.left = new TreeNode(4);
21    	binaryTree.root.right.left = new TreeNode(5);
22
23    	int heightOfTree = height(binaryTree.root);
24    	System.out.printf("Height of tree is %d", heightOfTree);
25    }
26    
27    public static int height(TreeNode root) {
28
29    	if (root == null)
30    		return -1;
31
32    	int leftHeight = height(root.left);
33    	int rightHeight = height(root.right);
34
35    	return Math.max(leftHeight, rightHeight) + 1;
36    }
37}

因此，在上面的代码中，一旦我们到达最底层的子节点，我们就将树的高度加1，并将结果返回给上一次调用。输出：树的高度是2 现在让我们以非递归的方式做同样的事情。

树的高度-迭代

要迭代地计算树的高度，我们只需计算树中的层数。

涉及的步骤

1.创建一个队列，并将树根添加到队列中。 2.将节点从队列中弹出并向下遍历队列，同时将子节点添加到队列中。 3.在每次迭代中，将最新的元素添加到队列中，并将(该元素的)下一级别的元素添加到队列中。 4.执行此操作，直到队列大小变为零。这将意味着下一个级别的元素为零。 5.对于每个遍历的标高，加1。

以下是计算树高的迭代程序。

 1public static int heightIteratively(TreeNode root) {
 2
 3    if (root == null)
 4        return -1;
 5
 6    Queue<TreeNode> queue = new LinkedList<>();
 7    queue.add(root);
 8    int height = -1;
 9
10    while (!queue.isEmpty()) {
11        int size = queue.size();
12
13        height++;
14
15        while (size > 0) {
16            TreeNode treeNode = queue.remove();
17
18            if (treeNode.left != null)
19                queue.add(treeNode.left);
20
21            if (treeNode.right != null)
22                queue.add(treeNode.right);
23
24            size--;
25        }
26    }
27    return height;
28}

上面的代码一直运行，直到队列不为空。而且，它不断添加下一级别的所有元素，同时从队列中删除当前级别的项目。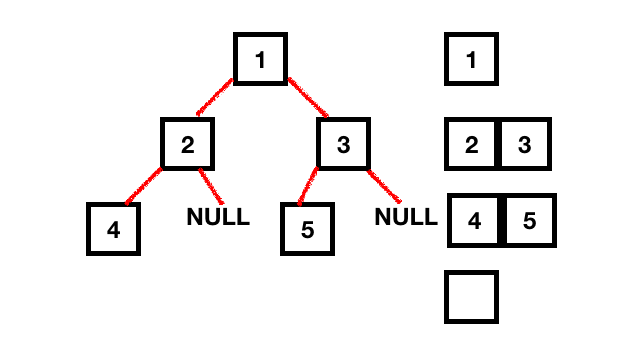

时间复杂度为O(N)。空间复杂度为O(1)。

您可以从我们的giHub Repository.]签出完整的代码和更多DS和算法示例

树形数据结构的高度

二叉树

树的高度-递归

树的高度-迭代