二叉树的高度被定义为从根节点开始的任何叶节点的最大深度。也就是说,它是从根节点到任何叶节点的最长路径的长度。
让我们考虑下面的二叉树。
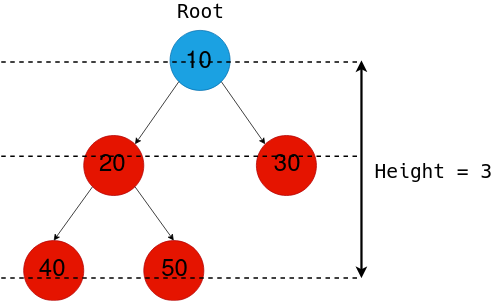
因为最大深度对应的叶节点是40 和** 50** ,所以要计算高度,我们只需找出从根节点到这两个节点中任何一个的边数,即3。
现在我们知道了二叉树的高度意味着什么,现在我们将构造一个算法来求出任何二叉树的高度。
C++中求二叉树高度的逻辑
现在让我们决定寻找高度背后的逻辑,并首先编写我们的伪代码。
我们将在树上使用递归,以求出高度。(有关概念,请参阅维基百科article)
由于树的高度被定义为从根到叶的最大路径,因此我们可以递归地计算左子树和右子树的高度。
我们现在可以在子树上应用高度的定义。
我们观察到它是左子树和右子树之间的最大值,然后加一。
因为树的高度是子树的最大高度+1 ,所以我们一直这样做,直到子树变成NULL,它的高度为0。
在这一点上,我们的函数将最终终止,
让我们编写计算高度的函数tree_Height()。
1// Find height of a tree, defined by the root node
2int tree_height(Node* root) {
3 if (root == NULL)
4 return 0;
5 else {
6 // Find the height of left, right subtrees
7 left_height = tree_height(root->left);
8 right_height = tree_height(root->right);
9
10 // Find max(subtree_height) + 1 to get the height of the tree
11 return max(left_height, right_height) + 1;
12}
当子树大小为0或根节点为NULL时,第3行评估终止条件。
第7行和第8行递归地找到左子树和右子树的高度。
最后,第11行返回两者中的最大值,返回树的高度。
C/C++实现
下面是一个完整的程序,显示了二叉树是如何构造的,然后显示了在tree_Height()中查找高度的逻辑。
1#include <stdio.h>
2#include <stdlib.h>
3
4typedef struct Node Node;
5
6// Define the Tree Node here
7struct Node {
8 int value;
9 // Pointers to the left and right children
10 Node* left, *right;
11};
12
13Node* init_tree(int data) {
14 // Creates the tree and returns the
15 // root node
16 Node* root = (Node*) malloc (sizeof(Node));
17 root->left = root->right = NULL;
18 root->value = data;
19 return root;
20}
21
22Node* create_node(int data) {
23 // Creates a new node
24 Node* node = (Node*) malloc (sizeof(Node));
25 node->value = data;
26 node->left = node->right = NULL;
27 return node;
28}
29
30void free_tree(Node* root) {
31 // Deallocates memory corresponding
32 // to every node in the tree.
33 Node* temp = root;
34 if (!temp)
35 return;
36 free_tree(temp->left);
37 free_tree(temp->right);
38 if (!temp->left && !temp->right) {
39 free(temp);
40 return;
41 }
42}
43
44int tree_height(Node* root) {
45 // Get the height of the tree
46 if (!root)
47 return 0;
48 else {
49 // Find the height of both subtrees
50 // and use the larger one
51 int left_height = tree_height(root->left);
52 int right_height = tree_height(root->right);
53 if (left_height >= right_height)
54 return left_height + 1;
55 else
56 return right_height + 1;
57 }
58}
59
60int main() {
61 // Program to demonstrate finding the height of a Binary Tree
62
63 // Create the root node having a value of 10
64 Node* root = init_tree(10);
65
66 // Insert nodes onto the tree
67 root->left = create_node(20);
68 root->right = create_node(30);
69 root->left->left = create_node(40);
70 root->left->right = create_node(50);
71
72 // Find the height of the tree
73 int height = tree_height(root);
74 printf("Height of the Binary Tree: %d\n", height);
75
76 // Free the tree!
77 free_tree(root);
78 return 0;
79}