在本文中,我们将学习如何使用C++解决分数背包问题。我们将从查看问题陈述开始,然后转到解决方案。这个问题是许多流行的经典问题之一。它与它的兄弟0-1背包和0-N knapsack.]有很大不同这是一种贪婪算法,另外两种是动态规划算法。
什么是分数背包?
_您会得到某些物品的重量和价格表,以及某个容量的袋子/背包,例如W。您的任务是装满这个袋子,使您在这个袋子中携带的所有物品的总价在所有配置下都是最高的。你可以收集任何物体作为一个整体,也可以是它的一部分。
分数背包算法
好的,让我们来看看解决这个问题的算法。由于我们将对此问题实施贪婪解决方案,下面是对贪婪算法的简要描述。
什么是贪婪算法?
在这些算法中,我们的目标是实现一个局部最大值/最小值在每一步,以实现一个全局最大值/最小值在最后。也就是说,我们最大化/最小化每个子问题的答案,它会引导我们找到整个问题的最大/最小答案。
‘注意:’你将要做出的贪婪的选择必须是安全的。
安全移动:如果存在可靠的初始移动的最佳答案,则该移动称为安全移动。
使用贪婪算法的策略
以下是开发一个完美的贪婪算法所应遵循的步骤。
- 做出贪婪的选择
- 证明这是一个
安全的举动,这样你就不会编写代码,最后发现这不是一个可行的选择。这一步是贪婪算法最重要的一步。 - 减少到较小的问题
- 解决所有较小的问题。

伪码
现在我们将一步一步地介绍背包算法。
- 按价值/重量比降序对物品进行排序。仅此一步就将选择最佳项的时间复杂度从
O(N)降低到O(Log2N)。 - 现在我们通过运行从i=0到i=N_的_for循环来开始选择对象
- ‘引理:’存在一个最优解,它尽可能多地使用单位重量值最大的物品。 -证明:尝试用不同的选择标准填充背包,您得到的总价值总是小于最大可能值。
下面的例子证明了我们的引理是正确的。
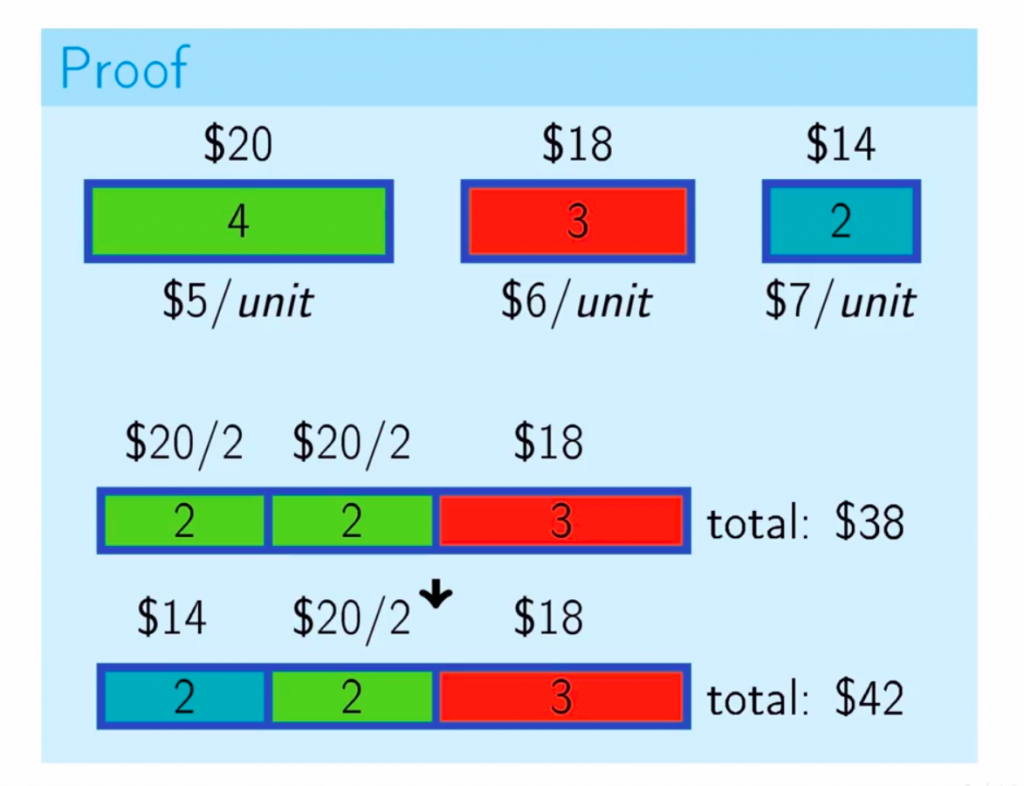
- 现在,如果具有最大价值/重量比的物品的大小适合背包,则将其全部拿走。否则,取它可能的最大部分。
- 根据所取物品的重量减少袋子的容量。
-如果是整项,则:
Capacity=Capacity-Weight[This_Item]。 -否则,由于背包变满,容量变为0。 - 将该项所取分数的价值加至总价值。
-如果取整条:
Total_Value+=Value[This_Item]-否则,Value+=Fraction_of_Weight_Take* Value[This_Item]。 - 若量能变为0,则脱离循环
伪代码的整体结构变为:

演示分数背包的# C++程序
1#include <iostream>
2#include <algorithm>
3#include <vector>
4
5using namespace std;
6
7// this custom comparator function will allow
8// us to compare our vector based on the
9// ratio of values to weights
10bool compare(pair <float, int> p1, pair <float, int> p2)
11{
12 return p1.first > p2.first;
13}
14
15int fractional_knapsack(vector <int> weights, vector <int> values, int capacity)
16{
17 int len = weights.size();
18 int total_value = 0;
19
20 // vector to store the items based on their value/weight ratios
21 vector <pair <float, int>> ratio(len, make_pair(0.0, 0));
22
23 for(int i = 0; i < len; i++)
24 ratio[i] = make_pair(values[i]/weights[i], i);
25
26 // now sort the ratios in non-increasing order
27 // for this purpose, we will use our custom
28 // comparator function
29 sort(ratio.begin(), ratio.end(), compare);
30
31 // start selecting the items
32 for(int i = 0; i < len; i++)
33 {
34 if(capacity == 0)
35 break;
36
37 int index = ratio[i].second;
38
39 if(weights[index] <= capacity)
40 {
41 // we item can fit into the knapsack
42 // hence take the whole of it
43 capacity -= weights[index];
44
45 // add the value of this item to the
46 // final answer
47 total_value += values[index];
48 }
49 else
50 {
51 // this item doesn't fit into the bag
52 // and thus we take a fraction of it
53 int value_to_consider = values[index] * (float(capacity)/float(weights[index]));
54 total_value += value_to_consider;
55 capacity = 0;
56 }
57 }
58
59 return total_value;
60}
61
62int main()
63{
64 cout << "Enter the weights of the items, press -1 to stop" << endl;
65
66 vector <int> weights;
67
68 while(true)
69 {
70 int weight;
71 cin >> weight;
72
73 if(weight == -1)
74 break;
75
76 weights.push_back(weight);
77 }
78
79 cout << "Enter the values of each item, press -1 to stop" << endl;
80
81 vector <int> values;
82
83 while(true)
84 {
85 int value;
86 cin >> value;
87
88 if(value == -1)
89 break;
90
91 values.push_back(value);
92 }
93
94 cout << "Enter the capacity of the knapsack" << endl;
95
96 int capacity;
97 cin >> capacity;
98
99 cout << "The maximum value possible based on current list is: " << fractional_knapsack(weights, values, capacity) << endl;
100}
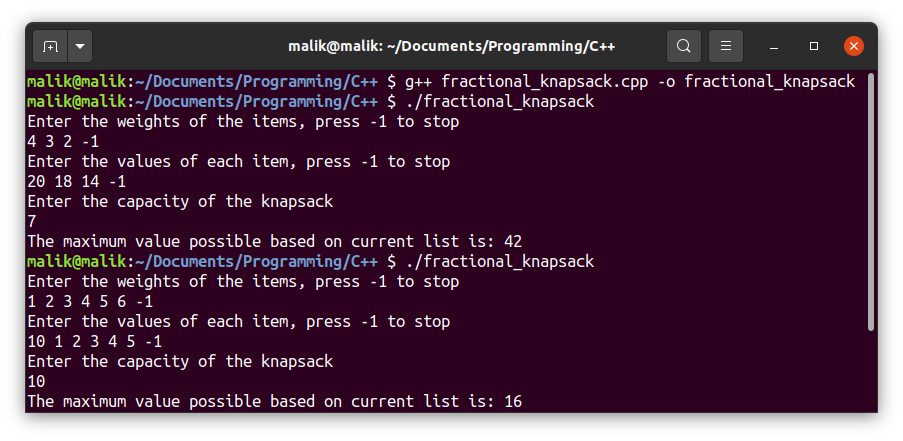
产出
结论
分数背包是一种贪婪的算法,在本文中,我们研究了它的实现。我们简单地学习了贪婪算法,然后讨论了分数背包算法的伪代码。我们证明了我们贪婪的选择是安全的,最后,我们编写了一个C++程序来演示这个解决方案。该概念的整体时间复杂度为:O(Nlog2N)。今天的节目到此结束,谢谢阅读。
进一步阅读
如果你想了解更多关于背包和其他贪婪算法的知识,你可以参考以下网站。