广度优先搜索 和** 深度优先搜索** 是两种遍历图和树的技术。在本教程中,我们将主要关注树中的BFS和DFS遍历。
什么是深度优先搜索?
该算法从根节点开始,然后探索backtracking.之前的每个分支它是使用堆栈实现的。在编写代码时,我们经常使用递归堆栈来回溯。通过使用递归,我们能够利用这样一个事实,即左子树和右子树也是树,并且共享相同的属性。
对于二叉树,有三种类型的DFS遍历。
1.有序 2.预购 3.后购
什么是广度优先搜索?
该算法也从根节点开始,然后逐级访问所有节点。这意味着在根之后,它将遍历根的所有直接子对象。在遍历根的所有直接子项之后,它将移动到它们的子项,依此类推。要实现BFS,我们使用队列。
对于二叉树,我们有层次顺序遍历 ,它遵循BFS。
BFS和DFS在Java中的实现
假设考虑中的树是:
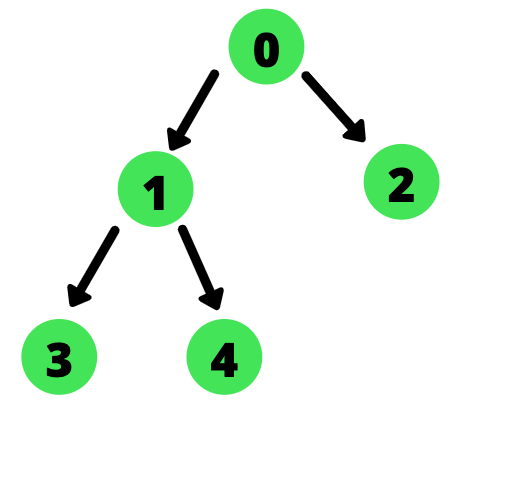
TreeNode类的结构如下:
1static class TreeNode {
2 int data;
3 TreeNode left, right;
4
5 public TreeNode(int key) {
6 data = key;
7 left = right = null;
8 }
9 }
1.预购遍历
在二叉树的预序遍历中,我们首先遍历根,然后遍历左子树,最后遍历右子树。我们递归地这样做是为了受益于左子树和右子树也是树这一事实。
预订单遍历的算法如下:
1.遍历根。 2.在左子树上调用preorder()。 3.在右子树上调用preorder()。
上述树的预购遍历为:
10 1 3 4 2
Java代码如下:
1static void preorder(TreeNode TreeNode) {
2 if (TreeNode == null)
3 return;
4
5 // Traverse root
6 System.out.print(TreeNode.item + "->");
7 // Traverse left
8 preorder(TreeNode.left);
9 // Traverse right
10 preorder(TreeNode.right);
11 }
2.有序遍历
二叉树的按序遍历首先遍历左子树,然后是根,最后是右子树。
有序遍历的算法如下:
1.对左子树调用inorder()。 2.遍历根。 3.对右子树调用inorder()。
上面树的顺序遍历是:
13 1 4 0 2
Java代码如下:
1static void inorder(TreeNode TreeNode) {
2 if (TreeNode == null)
3 return;
4
5 // Traverse left
6 inorder(TreeNode.left);
7 // Traverse root
8 System.out.print(TreeNode.item + "->");
9 // Traverse right
10 inorder(TreeNode.right);
11 }
3.订单后遍历
二叉树的后序遍历首先遍历左子树,然后遍历右子树,最后遍历根。
后序遍历的算法如下:
1.在左子树上调用postorder()。 2.对右子树调用postorder()。 3.遍历根。
上面树的后序遍历是:
13 4 1 2 0
Java代码如下:
1static void postorder(TreeNode TreeNode) {
2 if (TreeNode == null)
3 return;
4
5 // Traverse left
6 postorder(TreeNode.left);
7 // Traverse right
8 postorder(TreeNode.right);
9 // Traverse root
10 System.out.print(TreeNode.item + "->");
11 }
4.层次顺序遍历
层次顺序遍历使用队列来跟踪要访问的节点。访问一个节点后,它的子节点被放入队列中。为了得到一个新的节点来遍历,我们从队列中取出元素。
算法如下:
1.初始化空队列 2.从将temp设置为根开始 3.运行循环,直到队列不为空 1.从临时打印数据。 2.按从左到右的顺序排列临时员工的子项。 3.使节点从队列中退出队列,并将其值赋给Temp。
上述树的级别顺序遍历为:
10 1 2 3 4
Java代码如下:
1static void printLevelOrder(TreeNode root) {
2 Queue<TreeNode> queue = new LinkedList<TreeNode>();
3 queue.add(root);
4 while (!queue.isEmpty()) {
5 TreeNode temp = queue.poll();
6 System.out.print(temp.data + " ");
7
8 /*add left child to the queue */
9 if (temp.left != null) {
10 queue.add(temp.left);
11 }
12
13 /*add right right child to the queue */
14 if (temp.right != null) {
15 queue.add(temp.right);
16 }
17 }
18 }
用Java完成BFS和DFS的代码实现
完整的Java代码如下所示:
1package com.JournalDev;
2import java.util.LinkedList;
3import java.util.Queue;
4
5public class Main {
6 static class TreeNode {
7 int data;
8 TreeNode left, right;
9
10 public TreeNode(int key) {
11 data = key;
12 left = right = null;
13 }
14 }
15
16 static void preorder(TreeNode TreeNode) {
17 if (TreeNode == null)
18 return;
19
20 // Traverse root
21 System.out.print(TreeNode.data + " ");
22 // Traverse left
23 preorder(TreeNode.left);
24 // Traverse right
25 preorder(TreeNode.right);
26 }
27
28 static void inorder(TreeNode TreeNode) {
29 if (TreeNode == null)
30 return;
31
32 // Traverse left
33 inorder(TreeNode.left);
34 // Traverse root
35 System.out.print(TreeNode.data + " ");
36 // Traverse right
37 inorder(TreeNode.right);
38 }
39
40 static void postorder(TreeNode TreeNode) {
41 if (TreeNode == null)
42 return;
43
44 // Traverse left
45 postorder(TreeNode.left);
46 // Traverse right
47 postorder(TreeNode.right);
48 // Traverse root
49 System.out.print(TreeNode.data + " ");
50 }
51 static void printLevelOrder(TreeNode root) {
52 Queue<TreeNode> queue = new LinkedList<TreeNode>();
53 queue.add(root);
54 while (!queue.isEmpty()) {
55 TreeNode tempNode = queue.poll();
56 System.out.print(tempNode.data + " ");
57
58 /*add left child to the queue */
59 if (tempNode.left != null) {
60 queue.add(tempNode.left);
61 }
62
63 /*add right right child to the queue */
64 if (tempNode.right != null) {
65 queue.add(tempNode.right);
66 }
67 }
68 }
69
70 public static void main(String args[])
71
72 {
73 TreeNode root = new TreeNode(0);
74 root.left = new TreeNode(1);
75 root.right = new TreeNode(2);
76 root.left.left = new TreeNode(3);
77 root.left.right = new TreeNode(4);
78 System.out.println("Inorder traversal");
79 inorder(root);
80
81 System.out.println("\nPreorder traversal ");
82 preorder(root);
83
84 System.out.println("\nPostorder traversal");
85 postorder(root);
86
87 System.out.println("\nLevelorder traversal");
88 printLevelOrder(root);
89
90 }
91
92}
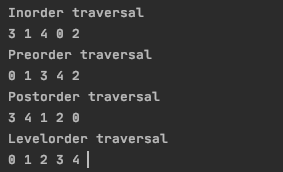
1Output :
2
3Inorder traversal
43 1 4 0 2
5Preorder traversal
60 1 3 4 2
7Postorder traversal
83 4 1 2 0
9Levelorder traversal
100 1 2 3 4
结论
本教程介绍的是二叉树中的BFS和DFS遍历。要获得C++中的DFS实现,请参阅此tutorial.有关级别顺序遍历的C++实现,请参阅此tutorial.