在二叉树的情况下,如果树是倾斜的,它们在执行操作上的计算效率就会变得很低。
这就是确保树木不倾斜背后的动机。因此,需要平衡二叉树。
什么是平衡二叉树
在平衡二叉树上执行操作在计算上是高效的。
平衡二叉树将遵循以下条件:
1.任意结点左右子树的高度绝对差小于1。 2.对于每个节点,其左子树是一棵平衡二叉树。 3.对于每个节点,其右子树是一棵平衡二叉树。
高度平衡二叉树
平衡二叉树也称为高度平衡二叉树。高度平衡二叉树可以表示为HB(K),其中k是左子树和右子树的高度差。‘k’被称为平衡系数。
如果对于一棵树,平衡因子(K)等于零,则该树称为完全平衡二叉树。它可以表示为HB(0) 。
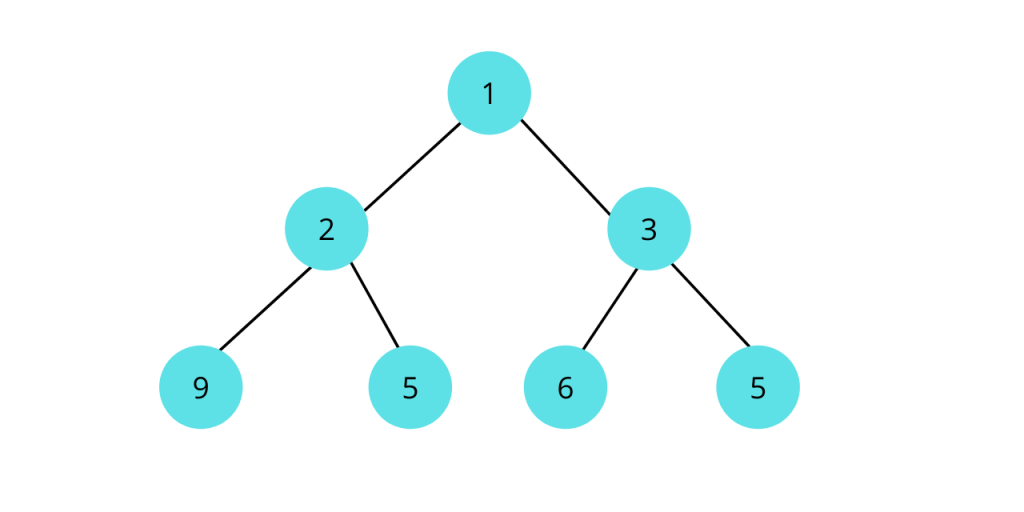
自平衡二叉查找树
如果一个二叉搜索树的平衡因子为1,则它是AVL(Adelso-Velskii and Landis) 树。这意味着在AVL树中,左子树和右子树之间的高度差至多为一。
AVL 树是一种自平衡的二叉树。在AVL树中,如果左子树和右子树之间的差异大于1,则它执行以下4个旋转之一来重新平衡自身:
- 左旋
- 向右旋转
- 左右旋转
- 左右旋转
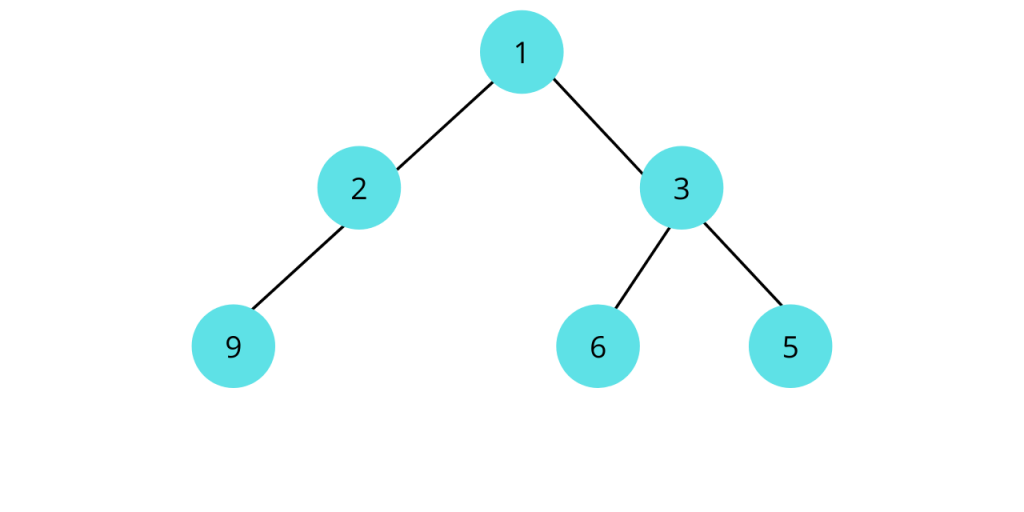
如何检查二叉树是否均衡?
要检查二叉树是否平衡,我们需要检查三个条件:
1.任意结点左右子树的高度绝对差应小于1。 2.对于每个节点,其左子树应该是平衡二叉树。 3.对于每个节点,其右子树应该是平衡二叉树。
我们需要一个函数,可以计算树的高度。一种方法是编写一个单独的函数来计算高度,并在每次需要高度时调用它。这在计算上将是低效的。
实现这一点的更好方法是在同一函数中返回Height。
对于每个节点,如果它不是平衡的,我们将返回-1,如果它是平衡的,则返回该节点/子树的高度。
算法如下:
- If node==NULL->返回0
- 选中左子树。如果不平衡->返回-1
- 勾选右子树。如果不平衡->返回-1
- 左右子树高度之间的绝对值。如果大于1->返回-1。
- 如果采油树是平衡的->返回高度
伪代码如下所示:
1private int balanceHeight (TreeNode currentNode)
2 {
3 if (currentNode == null)
4 {
5 return 0;
6 }
7
8 // checking left subtree
9 int leftSubtreeHeight = balanceHeight (currentNode.left);
10 if (leftSubtreeHeight == -1) return -1;
11 // if left subtree is not balanced then the entire tree is also not balanced
12
13 //checking right subtree
14 int rightSubtreeHeight = balanceHeight (currentNode.right);
15 if (rightSubtreeHeight == -1) return -1;
16 // if right subtree is not balanced then the entire tree is also not balanced
17
18 //checking the difference of left and right subtree for current node
19 if (Math.abs(leftSubtreeHeight - rightSubtreeHeight) > 1)
20 {
21 return -1;
22 }
23 //if it is balanced then return the height
24 return (Math.max(leftSubtreeHeight, rightSubtreeHeight) + 1);
25 }
您可以在树的根上调用此函数,如果它返回-1以外的任何值,则它是平衡二叉树。如果它返回-1,则它不是平衡二叉树。
总结
在本教程中,我们介绍了平衡二叉树以及如何检查树是否是平衡二叉树。希望你能理解并喜欢和我们一起学习。