简介
时间序列提供了预测未来价值的机会。根据以前的值,时间序列可以用来预测经济、天气和产能规划等方面的趋势。时间序列数据的特殊性意味着通常需要专门的统计方法。
在本教程中,我们将致力于产生可靠的时间序列预测。我们将首先介绍和讨论自相关性、平稳性和季节性的概念,然后继续应用时间序列预测最常用的方法之一,即ARIMA。
用来建模和预测时间序列的未来点的方法之一被称为SARIMAX ,它代表** 带有外生回归变量的季节性自回归综合移动平均线** 。在这里,我们将主要关注ARIMA组件,该组件用于拟合时间序列数据,以更好地理解和预测时间序列中的未来点。
前提条件
本指南将介绍如何在本地桌面或远程服务器上进行时间序列分析。处理大型数据集可能会占用大量内存,因此在任何一种情况下,计算机都需要至少 2GB内存 来执行本指南中的某些计算。
为了更好地理解本教程,熟悉一些时间序列和统计数据可能会有所帮助。
在本教程中,我们将使用Jupyter Notebook 来处理数据。如果您还没有,您应该按照我们的[教程]来安装和设置Jupyter Notebook for Python 3](https://andsky.com/tech/tutorials/how-to-set-up-jupyter-notebook-for-python-3).
第一步-安装包
要设置我们的时间序列预测环境,让我们首先进入我们的本地编程environment或基于服务器的编程environment:
1cd environments
1. my_env/bin/activate
从这里开始,让我们为我们的项目创建一个新目录。我们将其命名为ARIMA,然后移到目录中。如果您将项目命名为不同的名称,请务必在本指南中将您的名称替换为ARIMA
1mkdir ARIMA
2cd ARIMA
本教程将需要warnings、itertools、anda as、numpy、matplotlib和statsModels库。warnings和itertools库包含在标准的Python库集中,因此您应该不需要安装它们。
和其他的Python包一样,我们可以使用piap安装这些需求。
现在我们可以安装anda as、statsmods和数据绘制包matplotlib。还将安装它们的依赖项:
1pip install pandas numpy statsmodels matplotlib
此时,我们已经设置好开始使用已安装的包。
第二步-打包并加载数据
为了开始使用我们的数据,我们将启动Jupyter Notebook:
1jupyter notebook
要创建新的笔记本文件,请在右上角的下拉菜单中选择[新建]>[Python3]:
这将打开一个笔记本。
作为最佳实践,从导入笔记本顶部需要的libraries开始:
1import warnings
2import itertools
3import pandas as pd
4import numpy as np
5import statsmodels.api as sm
6import matplotlib.pyplot as plt
7plt.style.use('fivethirtyeight')
我们还为我们的地块定义了一个为FiveThirtyEight的`matplotlib‘style。
我们将使用一个名为美国夏威夷莫纳罗亚天文台连续空气样本中的大气二氧化碳的数据集,该数据集收集了1958年3月至2001年12月的二氧化碳样本。我们可以按如下方式引入此数据:
1data = sm.datasets.co2.load_pandas()
2y = data.data
在继续之前,让我们先对数据进行一点预处理。每周的数据可能很难处理,因为它的时间更短,所以让我们使用每月的平均数据。我们将使用resample函数进行转换。为简单起见,我们还可以使用fulna()function来确保我们的时间序列中没有遗漏的值。
1# The 'MS' string groups the data in buckets by start of the month
2y = y['co2'].resample('MS').mean()
3
4# The term bfill means that we use the value before filling in missing values
5y = y.fillna(y.bfill())
6
7print(y)
1[secondary_label Output]
2co2
31958-03-01 316.100000
41958-04-01 317.200000
51958-05-01 317.433333
6...
72001-11-01 369.375000
82001-12-01 371.020000
让我们将这个时间序列e作为一个数据可视化来探索:
1y.plot(figsize=(15, 6))
2plt.show()
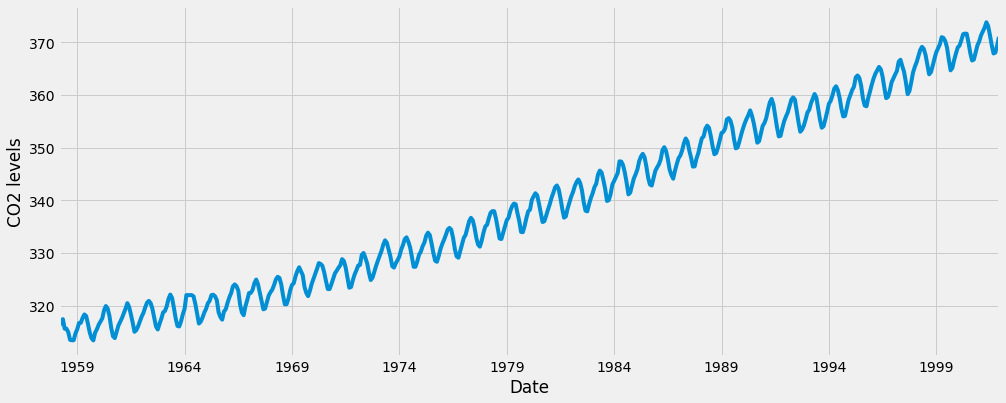
当我们绘制数据时,会出现一些可区分的模式。时间序列具有明显的季节性特征,且总体呈上升趋势。
要了解更多关于时间序列前处理的内容,请参考《使用PYTHON 3,实现时间序列可视化指南》,其中详细介绍了上述步骤。
现在我们已经转换和研究了我们的数据,让我们继续使用ARIMA进行时间序列预测。
第三步--ARIMA时间序列模型
时间序列预测中最常用的方法之一被称为ARIMA模型,它代表A utoreg** R** 遗传** I** 集成** M** 预测** A** 平均。ARIMA是一种可以与时间序列数据拟合的模型,以便更好地理解或预测序列中的未来点。
有三个不同的整数(p、d、q)用于ARIMA模型的参数化。因此,ARIMA模型用符号‘ARIMA(p,d,q)’表示。这三个参数一起考虑了数据集中的季节性、趋势和噪声:
p是模型的_自回归_部分。它允许我们将过去价值观的影响融入到我们的模型中。直觉上,这类似于说,如果过去3天天气一直很暖和,明天可能会变暖。d是该模型的_Integrated_部分。这包括模型中包含差值(即,要从当前值中减去的过去时间点的数量)以应用于时间序列的术语。直观地说,这类似于说,如果过去三天的温差非常小,明天可能是相同的温度。q是模型的_移动平均_部分。这允许我们将模型的误差设置为过去在先前时间点观察到的误差值的线性组合。
在处理季节性影响时,我们使用_季节性_ARIMA,表示为ARIMA(p,d,q)(P,D,q)s‘。这里,(p,d,q)是上述的非季节性参数,而(p,d,q)遵循相同的定义,但应用于时间序列的季节性分量。术语s‘是时间序列的周期(4’表示季度周期,12`表示年度周期,等等)。
季节性ARIMA方法可能看起来令人望而生畏,因为涉及到多个调整参数。在下一节中,我们将描述如何自动确定季节性ARIMA时间序列模型的最优参数集的过程。
第四步--ARIMA时间序列模型的参数选择
当希望用季节性ARIMA模型来拟合时间序列数据时,我们的第一个目标是找到ARIMA(p,d,q)(P,D,q)s的值,以优化感兴趣的度量。有许多指导方针和最佳实践可以实现这一目标,然而,ARIMA模型的正确参数化可能是一个艰苦的手动过程,需要领域专业知识和时间。其他统计编程语言如R‘提供了[自动解决此issue](https://www.rdocumentation.org/packages/forecast/versions/7.3/topics/auto.arima),的方法,但这些方法还没有移植到Python语言上。在本节中,我们将通过编写Python代码来解决此问题,以便以编程方式为ARIMA(p,d,q)(P,D,q)s‘时间序列模型选择最佳参数值。
我们将使用)’函数对新的季节性ARIMA模型进行拟合,并评估其整体质量。一旦我们研究了整个参数环境,我们的最佳参数集将是为我们感兴趣的标准产生最佳性能的参数集。让我们首先生成我们希望评估的各种参数组合:
1# Define the p, d and q parameters to take any value between 0 and 2
2p = d = q = range(0, 2)
3
4# Generate all different combinations of p, q and q triplets
5pdq = list(itertools.product(p, d, q))
6
7# Generate all different combinations of seasonal p, q and q triplets
8seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
9
10print('Examples of parameter combinations for Seasonal ARIMA...')
11print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[1]))
12print('SARIMAX: {} x {}'.format(pdq[1], seasonal_pdq[2]))
13print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[3]))
14print('SARIMAX: {} x {}'.format(pdq[2], seasonal_pdq[4]))
1[secondary_label Output]
2Examples of parameter combinations for Seasonal ARIMA...
3SARIMAX: (0, 0, 1) x (0, 0, 1, 12)
4SARIMAX: (0, 0, 1) x (0, 1, 0, 12)
5SARIMAX: (0, 1, 0) x (0, 1, 1, 12)
6SARIMAX: (0, 1, 0) x (1, 0, 0, 12)
我们现在可以使用上面定义的三元组参数来自动化对不同组合的ARIMA模型进行训练和评估的过程。在统计学和机器学习中,这个过程被称为模型选择的网格搜索(或超参数优化)。
在评估和比较采用不同参数的统计模型时,可以根据其与数据的拟合程度或准确预测未来数据点的能力对每个模型进行相互排名。我们将使用AIC(Akaike Information Critariation,阿凯克信息准则)值,该值可以通过使用statsModels拟合的ARIMA模型方便地返回。AIC衡量模型对数据的拟合程度,同时考虑到模型的整体复杂性。与使用较少特征来实现相同的拟合优度的模型相比,使用大量特征的模型将被赋予更高的AIC分数。因此,我们感兴趣的是找到产生最低AIC值的模型。
下面的代码块迭代参数组合,并使用statsModels中的SARIMAX函数来拟合相应的季节性ARIMA模型。这里,order参数指定了(p,d,q)参数,而easonative_order参数指定了季节ARIMA模型的(P,D,q,S)季节分量。在对每个SARIMAX()模型进行拟合后,代码打印出其各自的AIC分数。
1warnings.filterwarnings("ignore") # specify to ignore warning messages
2
3for param in pdq:
4 for param_seasonal in seasonal_pdq:
5 try:
6 mod = sm.tsa.statespace.SARIMAX(y,
7 order=param,
8 seasonal_order=param_seasonal,
9 enforce_stationarity=False,
10 enforce_invertibility=False)
11
12 results = mod.fit()
13
14 print('ARIMA{}x{}12 - AIC:{}'.format(param, param_seasonal, results.aic))
15 except:
16 continue
由于某些参数组合可能会导致数字错误规范,因此我们显式禁用了警告消息,以避免警告消息过载。这些错误规范还可能导致错误并引发异常,因此我们确保捕获这些异常并忽略导致这些问题的参数组合。
上面的代码应该会产生以下结果,这可能需要一些时间:
1[secondary_label Output]
2SARIMAX(0, 0, 0)x(0, 0, 1, 12) - AIC:6787.3436240402125
3SARIMAX(0, 0, 0)x(0, 1, 1, 12) - AIC:1596.711172764114
4SARIMAX(0, 0, 0)x(1, 0, 0, 12) - AIC:1058.9388921320026
5SARIMAX(0, 0, 0)x(1, 0, 1, 12) - AIC:1056.2878315690562
6SARIMAX(0, 0, 0)x(1, 1, 0, 12) - AIC:1361.6578978064144
7SARIMAX(0, 0, 0)x(1, 1, 1, 12) - AIC:1044.7647912940095
8...
9...
10...
11SARIMAX(1, 1, 1)x(1, 0, 0, 12) - AIC:576.8647112294245
12SARIMAX(1, 1, 1)x(1, 0, 1, 12) - AIC:327.9049123596742
13SARIMAX(1, 1, 1)x(1, 1, 0, 12) - AIC:444.12436865161305
14SARIMAX(1, 1, 1)x(1, 1, 1, 12) - AIC:277.7801413828764
我们的代码输出表明,SARIMAX(1,1,1)x(1,1,1,12)产生的最低AIC值为277.78。因此,在我们考虑过的所有模型中,我们应该认为这是最好的选择。
步骤5-拟合ARIMA时间序列模型
使用网格搜索,我们已经确定了一组参数,该参数集产生了与我们的时间序列数据最佳匹配的模型。我们可以继续更深入地分析这个特定的模型。
我们将首先将最佳参数值插入新的SARIMAX模型:
1mod = sm.tsa.statespace.SARIMAX(y,
2 order=(1, 1, 1),
3 seasonal_order=(1, 1, 1, 12),
4 enforce_stationarity=False,
5 enforce_invertibility=False)
6
7results = mod.fit()
8
9print(results.summary().tables[1])
1[secondary_label Output]
2==============================================================================
3 coef std err z P>|z| [0.025 0.975]
4------------------------------------------------------------------------------
5ar.L1 0.3182 0.092 3.443 0.001 0.137 0.499
6ma.L1 -0.6255 0.077 -8.165 0.000 -0.776 -0.475
7ar.S.L12 0.0010 0.001 1.732 0.083 -0.000 0.002
8ma.S.L12 -0.8769 0.026 -33.811 0.000 -0.928 -0.826
9sigma2 0.0972 0.004 22.634 0.000 0.089 0.106
10==============================================================================
从SARIMAX的输出中得到的asumy属性返回大量信息,但我们将把注意力集中在系数表上。coef栏显示每个特征的权重(即重要性)以及每个特征对时间序列的影响。P>|z|列告诉我们每个特征权重的重要性。在这里,每个权重都有一个小于或接近‘0.05’的p值,因此在我们的模型中保留所有这些权重是合理的。
在拟合季节性ARIMA模型(以及任何其他模型)时,运行模型诊断以确保没有违反模型所做的任何假设是很重要的。我们可以使用Plot_Diagnotics对象快速生成模型诊断信息,并调查任何异常行为。
1results.plot_diagnostics(figsize=(15, 12))
2plt.show()
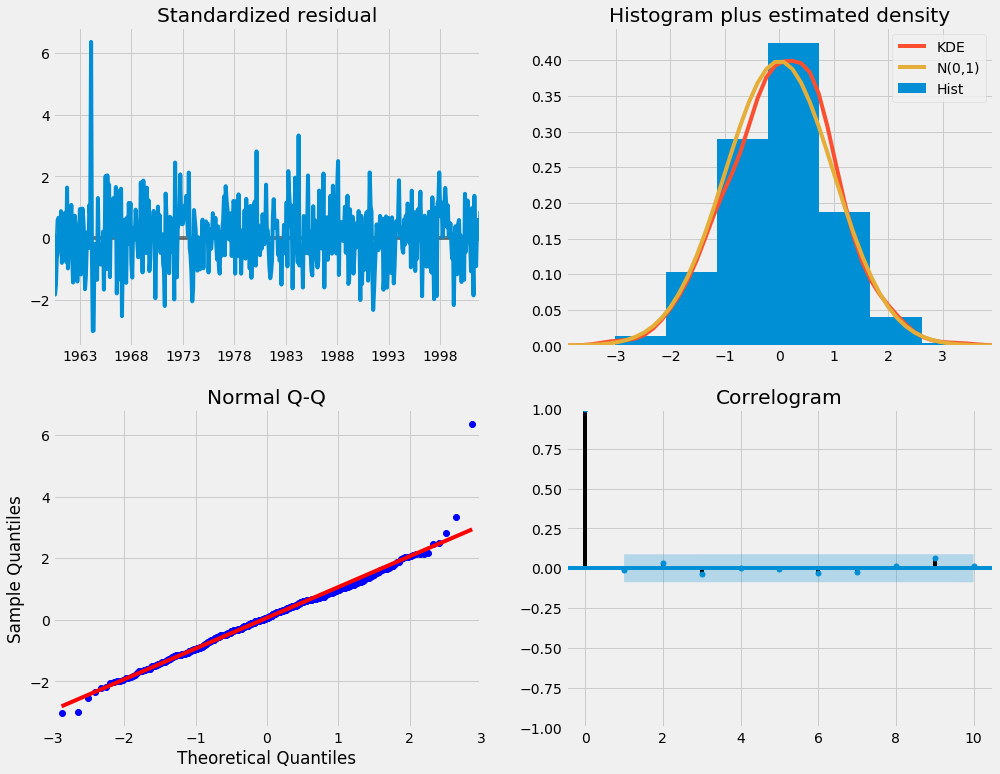
我们主要关注的是确保我们模型的残差是不相关的,并且正态分布为零均值。如果季节性ARIMA模型不满足这些性质,则表明它可以进一步改进。
在这种情况下,我们的模型诊断表明,模型残差基于以下条件正态分布:
- 在右上角的图中,我们看到红色的
KDE线紧跟着N(0,1)线(其中N(0,1)是正态分布的标准符号,平均值为0‘,标准差为1’)。这很好地表明了残差是正态分布的。 - 左下角的qq-plot显示,残差(蓝点)的有序分布遵循从标准正态分布获得的样本的线性趋势,其中N(0,1)`。再一次,这是残差呈正态分布的强烈迹象。
- 随时间变化的残差(左上图)没有显示任何明显的季节性,似乎是白噪声。右下角的自相关(即相关图)图证实了这一点,这表明时间序列残差与其自身的滞后版本的相关性较低。
这些观察使我们得出结论,我们的模型产生了令人满意的拟合,可以帮助我们理解我们的时间序列数据并预测未来的价值。
虽然我们有一个令人满意的拟合,我们的季节性ARIMA模型的一些参数可以改变,以改善我们的模型拟合。例如,我们的网格搜索只考虑了一组有限的参数组合,所以如果我们扩大网格搜索范围,我们可能会找到更好的模型。
第六步-验证预测
我们已经为我们的时间序列建立了一个模型,现在可以用来制作预测。我们首先将预测值与时间序列的实际值进行比较,这将有助于我们理解预测的准确性。通过get_recast()和conf_int()属性,我们可以获得时间序列预测的值和相关的置信度区间。
1pred = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=False)
2pred_ci = pred.conf_int()
上述代码要求预报从1998年1月开始。
`Dynamic=False‘参数确保我们提前一步生成预测,这意味着每个时间点的预测都是使用该时间点之前的完整历史生成的。
我们可以绘制二氧化碳时间序列的实际值和预测值,以评估我们做得有多好。请注意,我们如何通过切片日期索引来放大时间序列的末尾。
1ax = y['1990':].plot(label='observed')
2pred.predicted_mean.plot(ax=ax, label='One-step ahead Forecast', alpha=.7)
3
4ax.fill_between(pred_ci.index,
5 pred_ci.iloc[:, 0],
6 pred_ci.iloc[:, 1], color='k', alpha=.2)
7
8ax.set_xlabel('Date')
9ax.set_ylabel('CO2 Levels')
10plt.legend()
11
12plt.show()
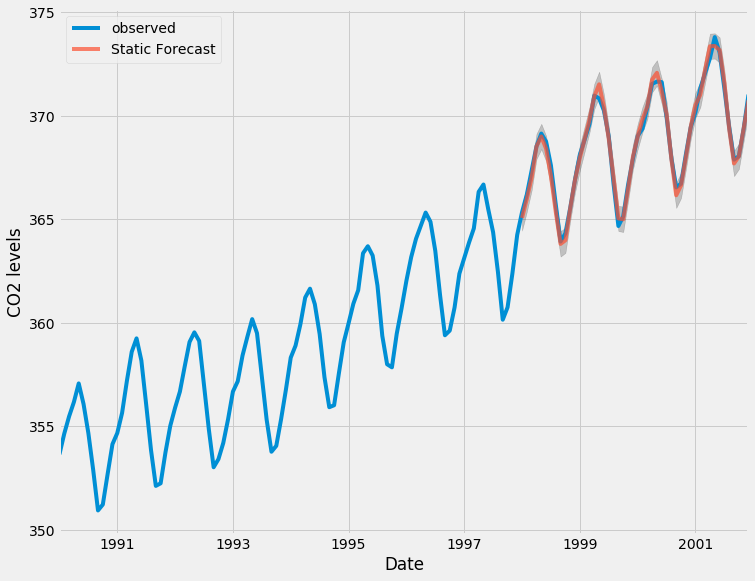
总体而言,我们的预测与真实值非常吻合,总体呈上升趋势。
它对量化我们预测的准确性也很有用。我们将使用MSE(均方误差),它总结了我们预测的平均误差。对于每个预测值,我们计算其与真实值的距离并将结果平方。需要对结果进行平方处理,以便在计算总体平均值时,正负差异不会相互抵消。
1y_forecasted = pred.predicted_mean
2y_truth = y['1998-01-01':]
3
4# Compute the mean square error
5mse = ((y_forecasted - y_truth) ** 2).mean()
6print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))
1[secondary_label Output]
2The Mean Squared Error of our forecasts is 0.07
我们预测的超前一步的均方误差为0.07,这是一个非常低的值,因为它接近0。如果均方误差为0,则表示估计者正在以完美的精度预测参数的观测值,这将是理想的情况,但通常不可能。
然而,使用动态预测可以更好地表示我们的真实预测能力。在这种情况下,我们只使用从时间序列到特定时间点的信息,在此之后,使用先前预测时间点的值生成预测。
在下面的代码块中,我们指定从1998年1月开始计算动态预测和可信区间。
1pred_dynamic = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=True, full_results=True)
2pred_dynamic_ci = pred_dynamic.conf_int()
绘制时间序列的观测值和预测值,我们可以看到,即使使用动态预测,总体预测也是准确的。所有预测值(红线)与地面实况(蓝线)非常接近,并且在我们预测的置信区间内。
1ax = y['1990':].plot(label='observed', figsize=(20, 15))
2pred_dynamic.predicted_mean.plot(label='Dynamic Forecast', ax=ax)
3
4ax.fill_between(pred_dynamic_ci.index,
5 pred_dynamic_ci.iloc[:, 0],
6 pred_dynamic_ci.iloc[:, 1], color='k', alpha=.25)
7
8ax.fill_betweenx(ax.get_ylim(), pd.to_datetime('1998-01-01'), y.index[-1],
9 alpha=.1, zorder=-1)
10
11ax.set_xlabel('Date')
12ax.set_ylabel('CO2 Levels')
13
14plt.legend()
15plt.show()

再一次,我们通过计算MSE来量化我们预测的预测性能:
1# Extract the predicted and true values of our time series
2y_forecasted = pred_dynamic.predicted_mean
3y_truth = y['1998-01-01':]
4
5# Compute the mean square error
6mse = ((y_forecasted - y_truth) ** 2).mean()
7print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))
1[secondary_label Output]
2The Mean Squared Error of our forecasts is 1.01
从动态预报获得的预测值产生的均方根误差为1.01。这略高于领先一步,这是意料之中的,因为我们对时间序列的历史数据依赖较少。
超前一步和动态预测都证实了这一时间序列模型的有效性。然而,围绕时间序列预测的兴趣很大程度上是预测未来价值的能力。
Step 7-预测的生成和可视化
在本教程的最后一步,我们将描述如何利用季节性ARIMA时间序列模型来预测未来值。我们的时间序列对象的get_forecast()属性可以计算未来指定步数的预测值。
1# Get forecast 500 steps ahead in future
2pred_uc = results.get_forecast(steps=500)
3
4# Get confidence intervals of forecasts
5pred_ci = pred_uc.conf_int()
我们可以使用这个代码的输出来绘制时间序列和对其未来值的预测。
1ax = y.plot(label='observed', figsize=(20, 15))
2pred_uc.predicted_mean.plot(ax=ax, label='Forecast')
3ax.fill_between(pred_ci.index,
4 pred_ci.iloc[:, 0],
5 pred_ci.iloc[:, 1], color='k', alpha=.25)
6ax.set_xlabel('Date')
7ax.set_ylabel('CO2 Levels')
8
9plt.legend()
10plt.show()
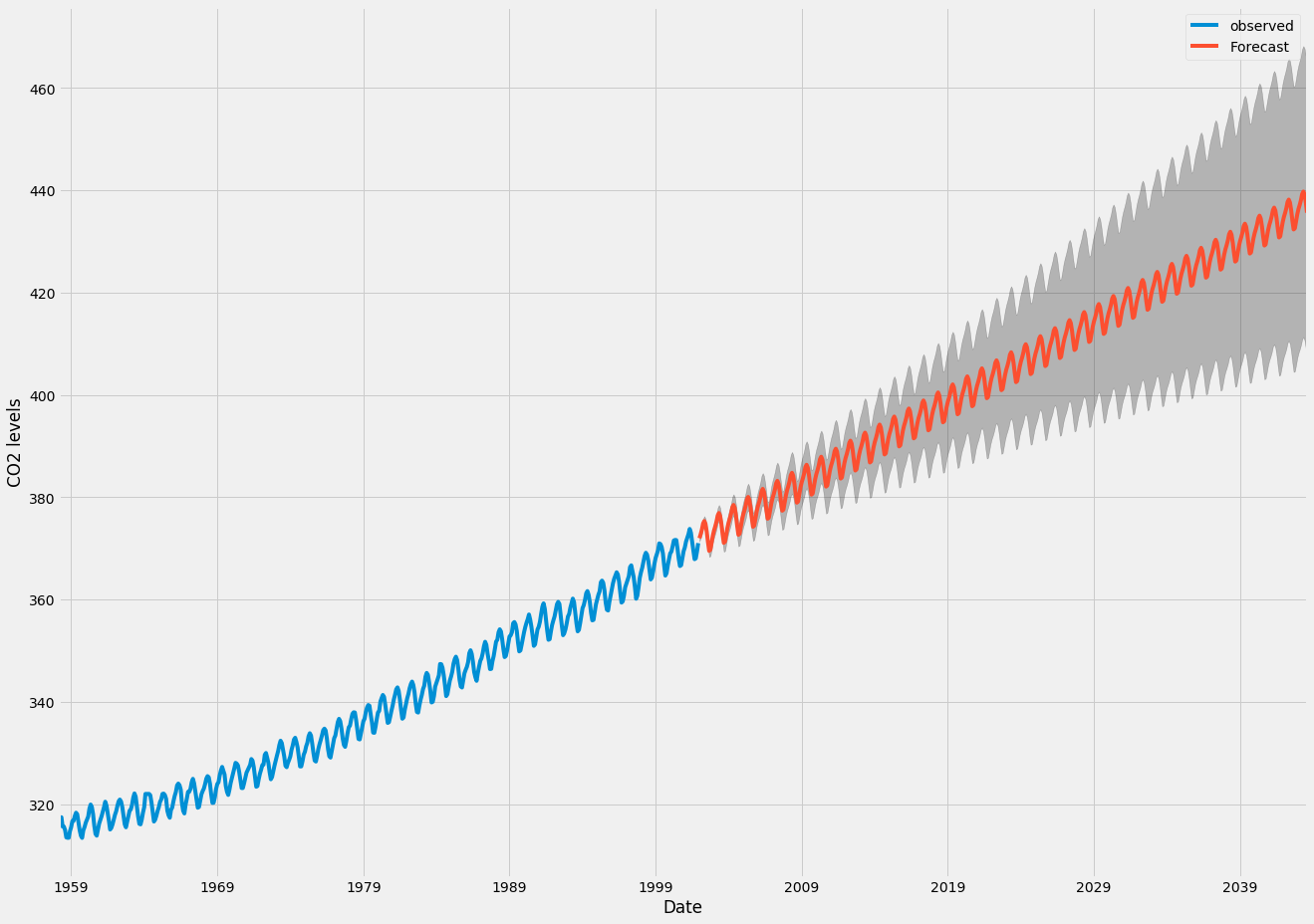 预测
预测
我们生成的预测和相关的可信区间现在都可以用来进一步了解时间序列和预见预期。我们的预测显示,预计时间序列将继续以稳定的速度增长。
正如我们对未来的预测一样,我们对自己的价值观变得不那么自信是很自然的。这一点反映在我们的模型产生的置信度区间,随着我们进一步深入未来,可信区间会变得更大。
结论
在本教程中,我们描述了如何在Python中实现季节性ARIMA模型。我们广泛使用了pandas和statsmodels库,并展示了如何运行模型诊断,以及如何生成CO2时间序列的预测。
以下是你可以尝试的其他几件事:
- 更改动态预测的开始日期,以查看这如何影响预测的总体质量。
- 尝试更多的参数组合,看看是否可以提高模型的拟合优度。
- 选择不同的度量以选择最佳模型。例如,我们使用
AIC度量来找到最佳模型,但您可以尝试优化样本外均方误差。
为了进行更多的实践,您还可以尝试加载另一个时间序列数据集来生成您自己的预测。